摘要：20． 证明:(1)∵AD∥BC.DE∥AB. ∴四边形ABED是平行四边形. ∴DE=AB． ∵AB=DC. ∴DE=DC． (2)∵AD∥BC.AB=DC.∠B=60°. ∴∠C-∠B-60∠． 又∵DE=DC. ∴△DEC是等边三角形．
网址：http://m.1010jiajiao.com/timu_id_8031[举报]
问题：在△ABC中，AB=AC，∠A=100°，BD为∠B 的平分线，探究AD、BD、BC之间的数量关系.
请你完成下列探究过程：
（1）观察图形，猜想AD、BD、BC之间的数量关系为 .
（2）在对（1）中的猜想进行证明时，当推出∠ABC=∠C=40°后，可进一步推出∠ABD=∠DBC= 度.
（3）为了使同学们顺利地解答本题（1）中的猜想，小强同学提供了一种探究的思路：在BC上截取BE=BD，连接DE,在此基础上继续推理可使问题得到解决.你可以参考小强的思路，画出图形，在此基础上对（1）中的猜想加以证明.也可以选用其它的方法证明你的猜想.
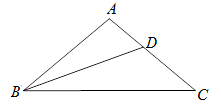
请你完成下列探究过程：
（1）观察图形，猜想AD、BD、BC之间的数量关系为 .
（2）在对（1）中的猜想进行证明时，当推出∠ABC=∠C=40°后，可进一步推出∠ABD=∠DBC= 度.
（3）为了使同学们顺利地解答本题（1）中的猜想，小强同学提供了一种探究的思路：在BC上截取BE=BD，连接DE,在此基础上继续推理可使问题得到解决.你可以参考小强的思路，画出图形，在此基础上对（1）中的猜想加以证明.也可以选用其它的方法证明你的猜想.
（本题满分10分）如图，梯形ABCD中，AD∥BC，CE⊥AB于E，BF⊥CD于F，连接AF、DE.
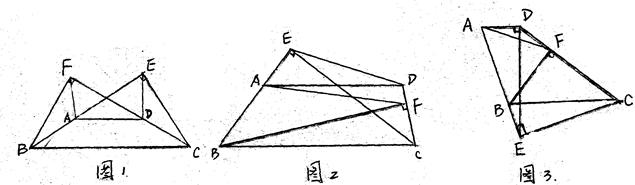
【小题1】(1)如图1，若AB=CD，且E、F两点分别在BA和CD的延长线上，在图中找出一个与∠BFA相等的角，如：∠BFA=
【小题2】(2)如图2，若AB≠CD，且E在BA的延长线上，F在CD上，则（1）的结论是否仍然成立？若成立，给出证明；若不成立，说明理由.
【小题3】(3)如图3，若AD⊥DE，AE=3AD，则tan∠BFA= 查看习题详情和答案>>
【小题1】(1)如图1，若AB=CD，且E、F两点分别在BA和CD的延长线上，在图中找出一个与∠BFA相等的角，如：∠BFA=
【小题2】(2)如图2，若AB≠CD，且E在BA的延长线上，F在CD上，则（1）的结论是否仍然成立？若成立，给出证明；若不成立，说明理由.
【小题3】(3)如图3，若AD⊥DE，AE=3AD，则tan∠BFA= 查看习题详情和答案>>
（本题满分10分）如图，梯形ABCD中，AD∥BC，CE⊥AB于E，BF⊥CD于F，连接AF、DE.
【小题1】(1)如图1，若AB=CD，且E、F两点分别在BA和CD的延长线上，在图中找出一个与∠BFA相等的角，如：∠BFA=
【小题2】(2)如图2，若AB≠CD，且E在BA的延长线上，F在CD上，则（1）的结论是否仍然成立？若成立，给出证明；若不成立，说明理由.
【小题3】(3)如图3，若AD⊥DE，AE=3AD，则tan∠BFA=
，以点C为圆心，CB为半径的弧交CA于点D；以点A为圆心，AD为半径的弧交AB于点E．