摘要:将A的坐标分别代入.
网址:http://m.1010jiajiao.com/timu_id_7955[举报]
解:(1)点C的坐标为![]() .
.
∵ 点A、B的坐标分别为![]() ,
,
∴ 可设过A、B、C三点的抛物线的解析式为![]() .
.
将![]() 代入抛物线的解析式,得
代入抛物线的解析式,得![]() .
.
∴ 过A、B、C三点的抛物线的解析式为![]() .
.
 (2)可得抛物线的对称轴为
(2)可得抛物线的对称轴为![]() ,顶点D的坐标为
,顶点D的坐标为
![]() ,设抛物线的对称轴与x轴的交点为G.
,设抛物线的对称轴与x轴的交点为G.
直线BC的解析式为![]() .
.
设点P的坐标为![]() .
.
解法一:如图8,作OP∥AD交直线BC于点P,
连结AP,作PM⊥x轴于点M.
∵ OP∥AD,
∴ ∠POM=∠GAD,tan∠POM=tan∠GAD.
∴ ![]() ,即
,即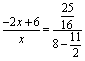 .
.
解得![]() . 经检验
. 经检验![]() 是原方程的解.
是原方程的解.
此时点P的坐标为![]() .
.
但此时![]() ,OM<GA.
,OM<GA.
∵ ![]()
∴ OP<AD,即四边形的对边OP与AD平行但不相等,
∴ 直线BC上不存在符合条件的点P. - - - - - - - - - - - - - - - - - - - - - 6分
解法二:如图9,取OA的中点E,作点D关于点E的对称点P,作PN⊥x轴于
点N. 则∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG .
由![]() ,可得E点的坐标为
,可得E点的坐标为![]() .
.
NE=EG=![]() , ON=OE-NE=
, ON=OE-NE=![]() ,NP=DG=
,NP=DG=![]() .
.
∴ 点P的坐标为![]() .∵ x=
.∵ x=![]() 时,
时,![]() ,
,
∴ 点P不在直线BC上.
∴ 直线BC上不存在符合条件的点P .

(3)![]() 的取值范围是
的取值范围是![]() .
.
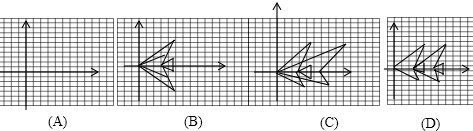
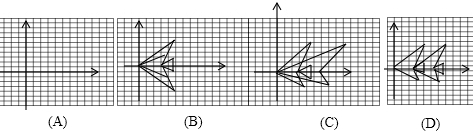
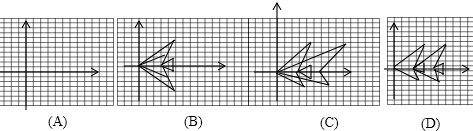
将点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0),在上面坐标系A中描出,并顺次连接画在A中.(对以下问题请将图形代码填入相应的括号内)
做如下变化:
(1)横坐标保持不变,纵坐标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案是
(2)纵坐标保持不变,横坐标分别变为原来的2倍,再将所得的 点用线段依次连接起来,所得的图案是
(3)纵坐标保持不变,横坐标分别加3,再将所得的 点用线段依次连接起来,所得的图案是
查看习题详情和答案>>
做如下变化:
(1)横坐标保持不变,纵坐标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案是
B
B
;(2)纵坐标保持不变,横坐标分别变为原来的2倍,再将所得的 点用线段依次连接起来,所得的图案是
C
C
;(3)纵坐标保持不变,横坐标分别加3,再将所得的 点用线段依次连接起来,所得的图案是
D
D
.