题目内容
25、小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:

(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.


(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

分析:(1)设y2=k(x-4)2+3.6,根据图象过点(0,2)可求k值,得解析式,再求当y=0时x的值就是水平距离;
(2)经过对以上推球方向与水平线夹角不同时,抛出的最远距离也不同进行分析可知沿45°夹角为最合理的.
(2)经过对以上推球方向与水平线夹角不同时,抛出的最远距离也不同进行分析可知沿45°夹角为最合理的.
解答:解:(1)
抛物线过点(0,2),代入y2=k(x-4)2+3.6,
得2=k(0-4)2+3.6,k=-0.1
∴y2=-0.1(x-4)2+3.6
而y2过点(x,0),
即y2=0时,有-0.1(x-4)2+3.6=0
解得:x=10
∴k=-0.1 x=10.
(2)用力适度情况下,尽力保持与水平方向45°角推铅球.
抛物线过点(0,2),代入y2=k(x-4)2+3.6,
得2=k(0-4)2+3.6,k=-0.1
∴y2=-0.1(x-4)2+3.6
而y2过点(x,0),
即y2=0时,有-0.1(x-4)2+3.6=0
解得:x=10
∴k=-0.1 x=10.
(2)用力适度情况下,尽力保持与水平方向45°角推铅球.
点评:认真审题和观察图象,求出y2的解析式是本题的关键.

练习册系列答案
相关题目
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
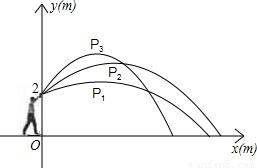
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2= ______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m | ______m | 7.3m |
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
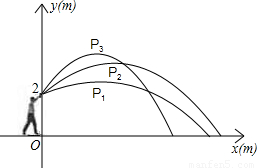
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2= ______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m | ______m | 7.3m |
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
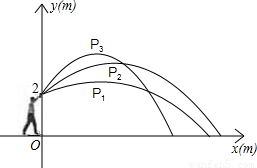
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2= ______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m | ______m | 7.3m |
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
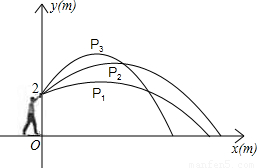
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2= ______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m | ______m | 7.3m |
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
