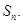摘要:已知数列和满足:,其中为实数.为正整数.(Ⅰ)对任意实数.证明数列不是等比数列,(Ⅱ)试判断数列是否为等比数列.并证明你的结论,(Ⅲ)设,为数列的前项和.是否存在实数.使得对任意正整数.都有?若存在.求的取值范围,若不存在.说明理由.解:本小题主要考查等比数列的定义.数列求和.不等式等基础知识和分类讨论的思想.考查综合分析问题的能力和推理认证能力.(Ⅰ)证明:假设存在一个实数λ.使{an}是等比数列.则有a22=a1a3,即矛盾.所以{an}不是等比数列.(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3n+1(an-2n+14)=(-1)n?(an-3n+21)=-bn又b1x-,所以当λ=-18.bn=0(n∈N+),此时{bn}不是等比数列:当λ≠-18时.b1= ≠0,由上可知bn≠0.∴(n∈N+).故当λ≠-18时.数列{bn}是以-为首项.-为公比的等比数列.知.当λ=-18,bn=0,Sn=0,不满足题目要求.∴λ≠-18.故知bn= -n-1.于是可得Sn=-要使a<Sn<b对任意正整数n成立.即a<-n]〈b(n∈N+) ①当n为正奇数时.1<f(n)∴f=,f= ,于是.由①式得a<-,<当a<b3a时.由-b-18=-3a-18.不存在实数满足题目要求,当b>3a存在实数λ.使得对任意正整数n,都有a<Sn<b,且λ的取值范围是
网址:http://m.1010jiajiao.com/timu_id_78265[举报]
(本小题满分14分)
已知数列{an}和{bn}满足:a1=λ,an+1=![]() 其中λ为实数,n为正整数。
其中λ为实数,n为正整数。
(Ⅰ)对任意实数λ,证明数列{an}不是等比数列;
(Ⅱ)试判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)设0<a<b,Sn为数列{bn}的前n项和。是否存在实数λ,使得对任意正整数n,都有
a<Sn<b?若存在,求λ的取值范围;若不存在,说明理由。
查看习题详情和答案>>(本小题满分14分)
已知数列{an}和{bn}满足:a1=λ,an+1=![]() 其中λ为实数,n为正整数。
其中λ为实数,n为正整数。
(Ⅰ)对任意实数λ,证明数列{an}不是等比数列;
(Ⅱ)试判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)设0<a<b,Sn为数列{bn}的前n项和。是否存在实数λ,使得对任意正整数n,都有
a<Sn<b?若存在,求λ的取值范围;若不存在,说明理由。
查看习题详情和答案>>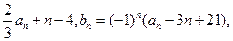 其中λ为实数,n为正整数。
其中λ为实数,n为正整数。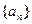 满足如图所示的程序框图.(Ⅰ)写出数列
满足如图所示的程序框图.(Ⅰ)写出数列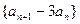 是等比数列,并求
是等比数列,并求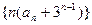 的前
的前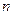 项和
项和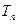 .
.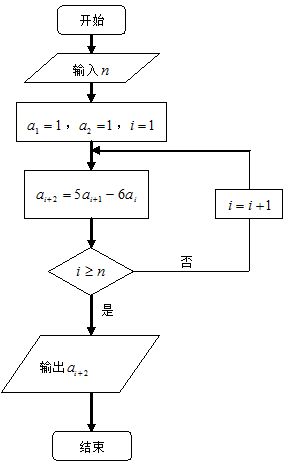
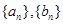 满足:
满足: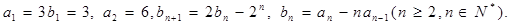
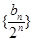 是等差数列还是等比数列,并由此求数列
是等差数列还是等比数列,并由此求数列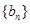 的通项公式;
的通项公式; 的前n项和
的前n项和