摘要：∵ ＝1+C×0.01+C×0.01+C×0.01+-≈1.1046
网址：http://m.1010jiajiao.com/timu_id_78182[举报]
例10．（2004年重庆卷）某工厂生产某种产品，已知该产品的月生产量（吨）与每吨产品的价格（元/吨）之间的关系式为：,且生产x吨的成本为（元）.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）
解：每月生产x吨时的利润为
，故它就是最大值点，且最大值为：
答：每月生产200吨产品时利润达到最大，最大利润为315万元.
已知y=x（x-1）（x+1）的图象如图所示．令f（x）=x（x-1）（x+1）+0.01，则下列关于f（x）=0的解叙述正确的是①⑤
①⑤
．①有三个实根；
②x＞1时恰有一实根；
③当0＜x＜1时恰有一实根；
④当-1＜x＜0时恰有一实根；
⑤当x＜-1时恰有一实根（有且仅有一实根）．
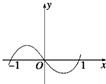9、已知y=x（x-1）（x+1）的图象如图所示，今考虑f（x）=x（x-1）（x+1）+0.01，则方程f（x）=0①有三个实根；②当x＜-1时，恰有一实根（有一实根且仅有一实根）；③当-1＜x＜0时，恰有一实根；④当0＜x＜1时，恰有一实根；⑤当x＞1时，恰有一实根．则正确结论的编号为
①②
．甲、乙两机床加工同一种零件，抽检得到它们加工后的零件尺寸x（单位：cm）及个数y如下表．
由表中数据得y关于x的线性回归方程为y=-91+100x（1.01≤x≤1.05），其中合格零件尺寸为1.03±0.01（cm）．
（1）是否有99%的把握认为加工零件的质量与甲、乙有关？
（2）从甲、乙加工后尺寸大于1.03cm的零件中各取1个，求恰好取到2个都是不合格零件的概率．
查看习题详情和答案>>
| 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | ||
| 零件尺寸x | 甲 | 3 | 7 | 8 | 9 | 3 |
| 零件个数y | 乙 | 7 | 4 | 4 | 4 | a |
（1）是否有99%的把握认为加工零件的质量与甲、乙有关？
（2）从甲、乙加工后尺寸大于1.03cm的零件中各取1个，求恰好取到2个都是不合格零件的概率．
已知y＝x(x－1)(x＋1)的图像如图所示，今考虑f(x)＝x(x－1)(x＋1)＋0.01，对于方程式f(x)＝0根的情况，以下说法正确的是________．(填上正确的序号)