摘要:例8.设.求函数的单调区间.分析:本小题主要考查导数的概念和计算.应用导数研究函数性质的方法及推理和运算能力. 解:. 当时 .(i)当时.对所有.有.即.此时在内单调递增.(ii)当时.对.有.即.此时在(0.1)内单调递增.又知函数在x=1处连续.因此.函数在(0.+)内单调递增(iii)当时.令.即.解得.因此.函数在区间内单调递增.在区间内也单调递增.令.解得.因此.函数在区间内单调递减.
网址:http://m.1010jiajiao.com/timu_id_78152[举报]
(本小题满分12分)设函数 ,曲线
,曲线 在点M
在点M 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求 的解析式;
(Ⅱ)求函数
的解析式;
(Ⅱ)求函数 的单调递减区间;
的单调递减区间;
(Ⅲ)证明:曲线 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
查看习题详情和答案>>
(本题12分)
设函数 ,曲线
,曲线 在点M
在点M 处的切线方程为
处的切线方程为 .
.
(1)求 的解析式; (2)求函数
的解析式; (2)求函数 的单调递减区间;
的单调递减区间;
(3)证明:曲线 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
查看习题详情和答案>>
(本题12分)
设函数 ,曲线
,曲线 在点M
在点M 处的切线方程为
处的切线方程为 .
.
(1)求 的解析式; (2)求函数
的解析式; (2)求函数 的单调递减区间;
的单调递减区间;
(3)证明:曲线 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
查看习题详情和答案>>
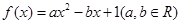 ,
,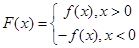
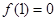 且对任意实数
且对任意实数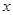 均有
均有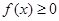 ,求
,求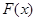 的解析式;
的解析式;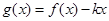 在区间
在区间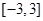 是单调函数,求实数
是单调函数,求实数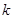 的取值范围;
的取值范围; 且
且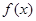 为偶函数,如果
为偶函数,如果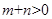 ,求证:
,求证: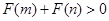 .
.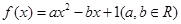 ,
,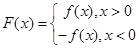
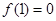 且对任意实数
且对任意实数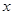 均有
均有 ,求
,求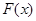 的解析式;
的解析式;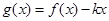 在区间
在区间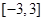 是单调函数,求实数
是单调函数,求实数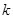 的取值范围;
的取值范围;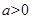 且
且 为偶函数,如果
为偶函数,如果 ,求证:
,求证: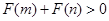 .
.