摘要:例2.已知PA⊥矩形ABCD所在平面.M.N分别是AB.PC的中点. (1)求证:MN⊥AB, (2)设平面PDC与平面ABCD所成的二面角为锐角θ.问能否确定θ使直线MN是异面直线AB与PC的公垂线?若能.求出相应θ的值,若不能.说明理由.解:(1)∵PA⊥矩形ABCD.BC⊥AB.∴PB⊥BC.PA⊥AC.即△PBC和△PAC都是以PC为斜边的直角三角形..又M为AB的中点.∴MN⊥AB.(2)∵AD⊥CD.PD⊥CD.∴∠PDA为所求二面角的平面角.即∠PDA=θ.设AB=a.PA=b.AD=d.则. 设PM=CM则由N为PC的中点.∴MN⊥PC由(1)可知MN⊥AB.∴MN为PC与AB的公垂线.这时PA=AD.∴θ=45°.(1)求证:AB1⊥平面CED,(2)求异面直线AB1与CD之间的距离,(3)求二面角B1―AC―B的平面角.解:(1)∵D是AB中点.△ABC为等腰直角三角形.∠ABC=900.∴CD⊥AB又AA1⊥平面ABC.∴CD⊥AA1.∴CD⊥平面A1B1BA ∴CD⊥AB1.又CE⊥AB1. ∴AB1⊥平面CDE,(2)由CD⊥平面A1B1BA ∴CD⊥DE∵AB1⊥平面CDE ∴DE⊥AB1,∴DE是异面直线AB1与CD的公垂线段∵CE=.AC=1 , ∴CD=∴,(3)连结B1C.易证B1C⊥AC.又BC⊥AC , ∴∠B1CB是二面角B1―AC―B的平面角.在Rt△CEA中.CE=.BC=AC=1,∴∠B1AC=600∴. ∴,∴ , ∴.说明:作出公垂线段和二面角的平面角是正确解题的前提, 当然, 准确地作出应当有严格的逻辑推理作为基石.
网址:http://m.1010jiajiao.com/timu_id_78006[举报]
 ,求证MN⊥面PCD.
,求证MN⊥面PCD.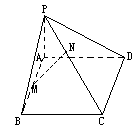
 如图,已知PA⊥矩形ABCD所在平面,M、N分别为AB、PC的中点;
如图,已知PA⊥矩形ABCD所在平面,M、N分别为AB、PC的中点; 已知PA⊥矩形ABCD所在平面,PA=AD,M、N分别是AB、PC的中点.
已知PA⊥矩形ABCD所在平面,PA=AD,M、N分别是AB、PC的中点. 如图,已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.
如图,已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.