题目内容
 如图,已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.
如图,已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
分析:(1)利用两平行线中的一条垂直于平面另一条也垂直平面判断出NO⊥平面ABCD,利用线面垂直的判定定理与性质定理得到MN⊥CD.
(2)利用等腰三角形的中线垂直于底边得到MN⊥PC,由(1)知,MN⊥CD,利用线面垂直的判定定理得到
MN⊥平面PCD.
(2)利用等腰三角形的中线垂直于底边得到MN⊥PC,由(1)知,MN⊥CD,利用线面垂直的判定定理得到
MN⊥平面PCD.
解答:证明:(1)连接AC,BD,设AC∩BD=0,连接NO,MO,则NO∥PA.

∵PA⊥平面ABCD,
∴NO⊥平面ABCD,
∴NO⊥AB,
∵MO⊥AB,
∴AB⊥面MNO
∴MN⊥AB,而CD∥AB,
∴MN⊥CD…(6分)
(2)∵∠PDA=45°
∴PA=AD=BC,由△PAM≌△CMB,
得PM=CM,
又∵N为PC的中点,
∴MN⊥PC
又MN⊥CD,PC∩CD=C
∴MN⊥平面PCD …(12分)

∵PA⊥平面ABCD,
∴NO⊥平面ABCD,
∴NO⊥AB,
∵MO⊥AB,
∴AB⊥面MNO
∴MN⊥AB,而CD∥AB,
∴MN⊥CD…(6分)
(2)∵∠PDA=45°
∴PA=AD=BC,由△PAM≌△CMB,
得PM=CM,
又∵N为PC的中点,
∴MN⊥PC
又MN⊥CD,PC∩CD=C
∴MN⊥平面PCD …(12分)
点评:本题考查线面垂直的判定定理;考查线面垂直的性质定理,利用三角形的中位线证明线线平行,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,已知PA⊥矩形ABCD所在平面,M、N分别为AB、PC的中点;
如图,已知PA⊥矩形ABCD所在平面,M、N分别为AB、PC的中点;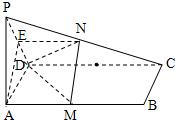 如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB,PC的中点;若P-CD-A为45°的二面角,求证:平面MND⊥平面PDC;
如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB,PC的中点;若P-CD-A为45°的二面角,求证:平面MND⊥平面PDC;
