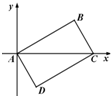
摘要:例5.如图,已知在矩形ABCD中,C(4,4),点A在曲线上移动,且AB,BC两边始终分别平行于x轴,y轴,求使矩形ABCD的面积为最小时点A的坐标.分析及解:设A(4-y) (1)此时S表示为变量x,y的函数,如何将S表示为一个变量x(或y)的函数呢?有的同学想到由已知得x2+y2=9,如何利用此条件?是从等式中解出x式,因为表达式有开方,显然此方法不好.如果我们将(1)式继续变形,会得到S=16-4(x+y)+xy (2)这时我们可联想到x2+y2与x+y.xy间的关系,即(x+y)2=9+2xy.因此,只需设t=x+y,则xy=,代入(2)式得 S=16-4t+(3)S表示为变量t的二次函数,∵0<x<3,0<y<3,∴3<t<,∴当t=4时,SABCD的最小值为.此时注:换元前后新旧变量的取值范围是不同的,这样才能防止出现不必要的错误.
网址:http://m.1010jiajiao.com/timu_id_77858[举报]
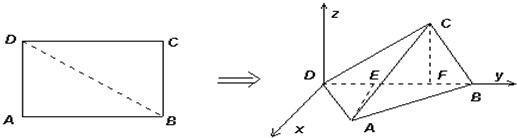
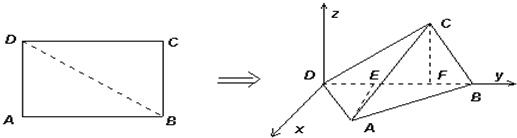
如图,已知矩形ABCD中,|AD|=3,|AB|=4.将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.
 查看习题详情和答案>>
查看习题详情和答案>>
 查看习题详情和答案>>
查看习题详情和答案>>