摘要:例4.若不等式对一切均成立.试求实数的取值范围.解: 令.则要使它对均有.只要有 或.点评:在有几个变量的问题中.常常有一个变元处于主要地位.我们称之为主元.由于思维定势的影响.在解决这类问题时.我们总是紧紧抓住主元不放.这在很多情况下是正确的.但在某些特定条件下.此路往往不通.这时若能变更主元.转移变元在问题中的地位.就能使问题迎刃而解.本题中.若视x为主元来处理.既繁且易出错.实行主元的转化.使问题变成关于p的一次不等式.使问题实现了从高维向低维转化.解题简单易行.
网址:http://m.1010jiajiao.com/timu_id_77850[举报]
设不等式组
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)
(1)求f(1),f(2)的值及f(n)的表达式;
(2)记Tn=
,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;
(3)设Sn为数列bn的前n项的和,其中bn=2f(n),问是否存在正整数n,t,使
<
成立?若存在,求出正整数n,t;若不存在,说明理由.
查看习题详情和答案>>
|
(1)求f(1),f(2)的值及f(n)的表达式;
(2)记Tn=
| f(n)•f(n+1) |
| 2n |
(3)设Sn为数列bn的前n项的和,其中bn=2f(n),问是否存在正整数n,t,使
| Sn+tbn |
| Sn+1-tbn+1 |
| 1 |
| 16 |
设不等式组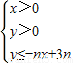 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)
(1)求f(1),f(2)的值及f(n)的表达式;
(2)记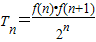 ,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;
,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;
(3)设Sn为数列bn的前n项的和,其中bn=2f(n),问是否存在正整数n,t,使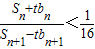 成立?若存在,求出正整数n,t;若不存在,说明理由.
成立?若存在,求出正整数n,t;若不存在,说明理由.
查看习题详情和答案>>
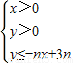 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)(1)求f(1),f(2)的值及f(n)的表达式;
(2)记
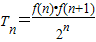 ,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;
,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;(3)设Sn为数列bn的前n项的和,其中bn=2f(n),问是否存在正整数n,t,使
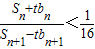 成立?若存在,求出正整数n,t;若不存在,说明理由.
成立?若存在,求出正整数n,t;若不存在,说明理由.查看习题详情和答案>>
设不等式组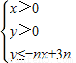 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)
(1)求f(1),f(2)的值及f(n)的表达式;
(2)记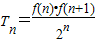 ,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;
,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;
(3)设Sn为数列bn的前n项的和,其中bn=2f(n),问是否存在正整数n,t,使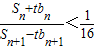 成立?若存在,求出正整数n,t;若不存在,说明理由.
成立?若存在,求出正整数n,t;若不存在,说明理由.
查看习题详情和答案>>
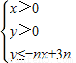 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)(1)求f(1),f(2)的值及f(n)的表达式;
(2)记
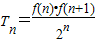 ,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;
,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;(3)设Sn为数列bn的前n项的和,其中bn=2f(n),问是否存在正整数n,t,使
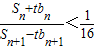 成立?若存在,求出正整数n,t;若不存在,说明理由.
成立?若存在,求出正整数n,t;若不存在,说明理由.查看习题详情和答案>>
 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)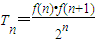 ,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;
,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;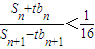 成立?若存在,求出正整数n,t;若不存在,说明理由.
成立?若存在,求出正整数n,t;若不存在,说明理由.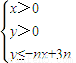 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n),(n∈N*)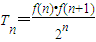 ,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;
,试比较Tn与Tn+1的大小;若对于一切的正整数n,总有Tn≤m成立,求实数m的取值范围;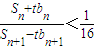 成立?若存在,求出正整数n,t;若不存在,说明理由.
成立?若存在,求出正整数n,t;若不存在,说明理由.