摘要: (提示:对a分:两种情况讨论)
网址:http://m.1010jiajiao.com/timu_id_77837[举报]
已知函数 , 其中
, 其中 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求曲线
时,求曲线 的单调区间与极值.
的单调区间与极值.
【解析】第一问中利用当 时,
时, ,
,
 ,得到切线方程
,得到切线方程
第二问中,

对a分情况讨论,确定单调性和极值问题。
解: (1) 当 时,
时, ,
,
 ………………………….2分
………………………….2分

 切线方程为:
切线方程为:  …………………………..5分
…………………………..5分
(2) 
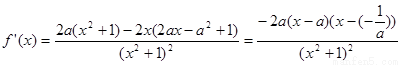 …….7
…….7 分
分
分类: 当 时, 很显然
时, 很显然
 的单调增区间为:
的单调增区间为:  单调减区间:
单调减区间:  ,
,
 ,
,  ………… 11分
………… 11分
当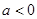 时
时 的单调减区间:
的单调减区间:  单调增区间:
单调增区间: 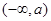 ,
,

 ,
, 
查看习题详情和答案>>
某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
)在某一个周期内的图象时,列表并填人的部分数据如下表:
(1)请将上表数据补全,并直接写出函数f(x)的解析式;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,若f(A)=2,sinB=2sinC,a=
,求b,c.
查看习题详情和答案>>
| π |
| 2 |
| x |
|
|
|||||||
| ωx+φ | 0 |
|
π |
|
2π | ||||
| Asin(ωx+φ) | 0 | 2 | 0 | -2 |
(2)在△ABC中,角A,B,C的对边分别是a,b,c,若f(A)=2,sinB=2sinC,a=
| 3 |