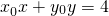摘要：例3.已知圆x2+y2=4.求经过点P(2.4).且与圆相切的直线方程. 分析:容易想到设出直线的点斜式方程y-4=k(x-2)再利用直线与圆相切的充要条件:“圆心到切线的距离等于圆的半径 .待定斜率k.从而得到所求直线方程.但要注意到:过点P的直线中.有斜率不存在的情形.这种情形的直线是否也满足题意呢?因此本题对过点P的直线分两种情形:斜率不存在- 解(略):所求直线方程为3x-4y+10=0或x=2

网址：http://m.1010jiajiao.com/timu_id_77805[举报]

已知圆x²+y²=4内一定点M（0，1），经M且斜率存在的直线交圆于A（x₁，y₁）、B（x₂，y₂）两点，过点A、B分别作圆的切线l₁，l₂．设切线l₁，l₂交于点Q．
（1）设点P（x₀，y₀）是圆上的点，求证：过P的圆的切线方程是 $数学公式$
（2）求证Q在一定直线上．

查看习题详情和答案>>

已知圆x²+y²=4内一定点M（0，1），经M且斜率存在的直线交圆于A（x₁，y₁）、B（x₂，y₂）两点，过点A、B分别作圆的切线l₁，l₂．设切线l₁，l₂交于点Q．
（1）设点P（x，y）是圆上的点，求证：过P的圆的切线方程是

（2）求证Q在一定直线上．
查看习题详情和答案>>

已知圆的方程和P点坐标，求经过P点的圆的切线方程．
（1）（x+2）²+（y-3）²=13，P（1，5）；
（2）x²+y²=9，P（3，4）．查看习题详情和答案>>

已知圆C1：x2+y2-2ay+a2-1=0与圆C2：(x-3)2+(y+2)2=16外切
（1）求实数a的值；
（2）若a＞0，求经过点P（-1，4）且与圆C₁相切的直线l的方程．

查看习题详情和答案>>

试题分类