题目内容
已知圆x2+y2=4内一定点M(0,1),经M且斜率存在的直线交圆于A(x1,y1)、B(x2,y2)两点,过点A、B分别作圆的切线l1,l2.设切线l1,l2交于点Q.(1)设点P(x,y)是圆上的点,求证:过P的圆的切线方程是

(2)求证Q在一定直线上.
【答案】分析:(1)当P不在坐标轴上时,求得切线的斜率,用点斜式求得切线方程,当P在x、y轴上时,经检验也满足,从而得出结论.
(2)设直线AB的方程为y=kx+1,代入x2+y2=4得(1+k2)x2+2kx-3=0,利用一元二次方程根与系数的关系以及(1)的结论求得Q(x,y)的坐标,可得Q(x,y)的坐标满足直线y=4的方程,从而得出结论.
解答:解:(1)当P不在坐标轴上时,OP的斜率为 ,故切线的斜率为
,故切线的斜率为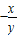 ,故切线方程为
,故切线方程为 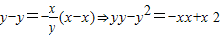 ,
,
又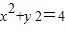 ,可得
,可得 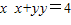 .
.
当P在y轴上时,P(0,2)或P(0,-2),此时切线方程为y=2或y=-2,上述方程也满足.
同理可得,当P在x上时上述方程也满足,
综上,原命题得证.
(2)设直线AB的方程为y=kx+1,
代入x2+y2=4得(1+k2)x2+2kx-3=0,∴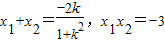 (定值).
(定值).
设Q(x,y),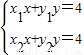 ,解得
,解得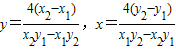 .
.
把y1=kx1+1,y2=kx2+1代入得:y=4,x=-4k.
故Q在一定直线y=4上.
点评:本题主要考查求圆的切线方程,一元二次方程根与系数的关系,直线过定点问题,属于中档题.
(2)设直线AB的方程为y=kx+1,代入x2+y2=4得(1+k2)x2+2kx-3=0,利用一元二次方程根与系数的关系以及(1)的结论求得Q(x,y)的坐标,可得Q(x,y)的坐标满足直线y=4的方程,从而得出结论.
解答:解:(1)当P不在坐标轴上时,OP的斜率为
 ,故切线的斜率为
,故切线的斜率为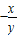 ,故切线方程为
,故切线方程为 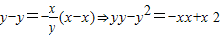 ,
,又
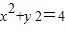 ,可得
,可得 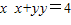 .
.当P在y轴上时,P(0,2)或P(0,-2),此时切线方程为y=2或y=-2,上述方程也满足.
同理可得,当P在x上时上述方程也满足,
综上,原命题得证.
(2)设直线AB的方程为y=kx+1,
代入x2+y2=4得(1+k2)x2+2kx-3=0,∴
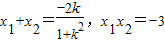 (定值).
(定值).设Q(x,y),
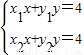 ,解得
,解得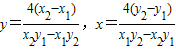 .
.把y1=kx1+1,y2=kx2+1代入得:y=4,x=-4k.
故Q在一定直线y=4上.
点评:本题主要考查求圆的切线方程,一元二次方程根与系数的关系,直线过定点问题,属于中档题.

练习册系列答案
相关题目