摘要:例17.对任意θ∈(0.)都有(A)sin<cosθ<cos (B) sin>cosθ>cos(C)sin<cosθ (D) sin<cosθ<cos解:当θ0时.sin0.cosθ1.coscos1.故排除A.B.当θ时.coscos1.cosθ0.故排除C.因此选D.
网址:http://m.1010jiajiao.com/timu_id_77704[举报]
对任意θ∈(0,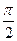 )都有( )
)都有( )
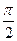 )都有( )
)都有( )| A.sin(sinθ)<cosθ<cos(cosθ) | B.sin(sinθ)>cosθ>cos(cosθ) |
| C.sin(cosθ)<cos(sinθ)<cosθ | D.sin(cosθ)<cosθ<cos(sinθ) |
28、(1)一次函数f(x)=kx+h(k≠0),若m<n有f(m)>0,f(n)>0,则对于任意x∈(m,n)都有f(x)>0,试证明之;
(2)试用上面结论证明下面的命题:若a,b,c∈R且|a|<1,|b|<1,|c|<1,则ab+bc+ca>-1.
查看习题详情和答案>>
(2)试用上面结论证明下面的命题:若a,b,c∈R且|a|<1,|b|<1,|c|<1,则ab+bc+ca>-1.
(理)已知二次函数f(x)=ax2+bx+c,(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,f(-2)=0,且当x∈(1,3)时,有f(x)≤
(x+2)2成立.
(1)求f(x)的表达式.
(2)g(x)=4f′(x)-sinx-2数列{an}满足:an+1=g(an),0<a1<1,n=1,2,3,证明:(Ⅰ)0<an+1<an<1;(Ⅱ)an+1<
an3.
查看习题详情和答案>>
| 1 |
| 8 |
(1)求f(x)的表达式.
(2)g(x)=4f′(x)-sinx-2数列{an}满足:an+1=g(an),0<a1<1,n=1,2,3,证明:(Ⅰ)0<an+1<an<1;(Ⅱ)an+1<
| 1 |
| 6 |