摘要:8.以1+与1-为根的一元二次方程的是
网址:http://m.1010jiajiao.com/timu_id_775223[举报]
若![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,则方程的两个根
的两个根,则方程的两个根![]() 和系数
和系数![]() 有如下关系:
有如下关系:![]() . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数![]() 的图象与x轴的两个交点为
的图象与x轴的两个交点为![]() .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:

请你参考以上定理和结论,解答下列问题:
设二次函数![]() 的图象与x轴的两个交点为
的图象与x轴的两个交点为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,显然
,显然![]() 为等腰三角形.
为等腰三角形.
(1)当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求
(2)当![]() 为等边三角形时,求
为等边三角形时,求![]()
查看习题详情和答案>>
已知一元二次方程x2+ax+a-2=0.
(1)求证:不论a为何实数,此方程总有两个不相等的实数根;
(2)设a<0,当二次函数y=x2+ax+a-2的图象与x轴的两个交点的距离为![]() 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;
(3)在(2)的条件下,若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为![]() ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由.
【解析】(1)判断上述方程的根的情况,只要看根的判别式△=b2-4ac的值的符号就可以了,(2)根据二次函数图象与x轴的两个交点的距离公式解答即可.(3)是二次函数综合应用问题和三角形的综合应用
查看习题详情和答案>>
若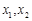 是关于
是关于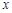 的一元二次方程
的一元二次方程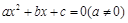 的两个根,则方程的两个根
的两个根,则方程的两个根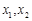 和系数
和系数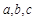 有如下关系:
有如下关系: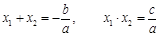 . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数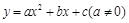 的图象与x轴的两个交点为
的图象与x轴的两个交点为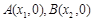 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
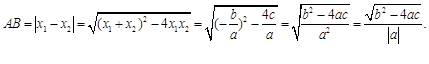
请你参考以上定理和结论,解答下列问题:
设二次函数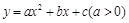 的图象与x轴的两个交点为
的图象与x轴的两个交点为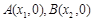 ,抛物线的顶点为
,抛物线的顶点为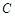 ,显然
,显然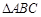 为等腰三角形.
为等腰三角形.
(1)当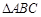 为等腰直角三角形时,求
为等腰直角三角形时,求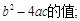
(2)当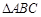 为等边三角形时,求
为等边三角形时,求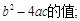 查看习题详情和答案>>
查看习题详情和答案>>
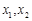 是关于
是关于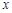 的一元二次方程
的一元二次方程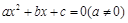 的两个根,则方程的两个根
的两个根,则方程的两个根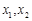 和系数
和系数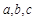 有如下关系:
有如下关系: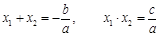 . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数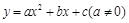 的图象与x轴的两个交点为
的图象与x轴的两个交点为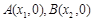 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为: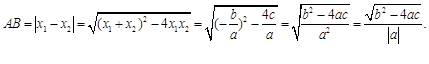
请你参考以上定理和结论,解答下列问题:
设二次函数
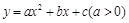 的图象与x轴的两个交点为
的图象与x轴的两个交点为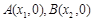 ,抛物线的顶点为
,抛物线的顶点为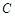 ,显然
,显然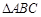 为等腰三角形.
为等腰三角形.(1)当
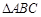 为等腰直角三角形时,求
为等腰直角三角形时,求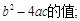
(2)当
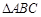 为等边三角形时,求
为等边三角形时,求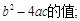 查看习题详情和答案>>
查看习题详情和答案>>
 是关于
是关于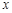 的一元二次方程
的一元二次方程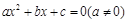 的两个根,则方程的两个根
的两个根,则方程的两个根 有如下关系:
有如下关系: . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数 的图象与x轴的两个交点为
的图象与x轴的两个交点为 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
 的图象与x轴的两个交点为
的图象与x轴的两个交点为 ,显然
,显然 为等腰三角形.
为等腰三角形.
 是关于
是关于 的一元二次方程
的一元二次方程 的两个根,则方程的两个根
的两个根,则方程的两个根 有如下关系:
有如下关系: .
我们把它们称为根与系数关系定理. 如果设二次函数
.
我们把它们称为根与系数关系定理. 如果设二次函数 的图象与x轴的两个交点为
的图象与x轴的两个交点为 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
 的图象与x轴的两个交点为
的图象与x轴的两个交点为 ,显然
,显然 为等腰三角形.
为等腰三角形.