摘要:23.选修4-4,坐标系与参数方程已知曲线C1:.曲线C2:.(Ⅰ)指出C1.C2各是什么曲线.并说明C1与C2公共点的个数,(Ⅱ)若把C1.C2上各点的纵坐标都压缩为原来的一半.分别得到曲线.写出的参数方程.与公共点的个数和C公共点的个数是否相同?说明你的理由.解:(Ⅰ)是圆.是直线.的普通方程为.圆心.半径.的普通方程为.因为圆心到直线的距离为.所以与只有一个公共点.(Ⅱ)压缩后的参数方程分别为:.化为普通方程为::.:.联立消元得.其判别式.所以压缩后的直线与椭圆仍然只有一个公共点.和与公共点个数相同.
网址:http://m.1010jiajiao.com/timu_id_77462[举报]
(本小题满分10分)选修4-4;坐标系与参数方程
在直角坐标第![]() 中,直线
中,直线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数),若以
为参数),若以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线![]() 的极坐标方程为
的极坐标方程为![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 所截的弦长。
所截的弦长。
(本小题满分10分)选修4-4;坐标系与参数方程
在直角坐标第![]() 中,直线
中,直线![]() 的参数方程为:
的参数方程为: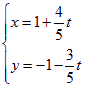 (
(![]() 为参数),若以
为参数),若以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线![]() 的极坐标方程为
的极坐标方程为![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 所截的弦长。
所截的弦长。
(本小题满分10分)选修4-4;坐标系与参数方程
在直角坐标第![]() 中,直线
中,直线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数),若以
为参数),若以![]() 为极点,
为极点,![]() 轴正半轴
轴正半轴
为极轴建立极坐标系,则曲线![]() 的极坐标方程为
的极坐标方程为![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 所截的弦长。
所截的弦长。
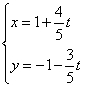 (
( 中,直线
中,直线 的参数方程为:
的参数方程为: (
( 为参数),若以
为参数),若以 为极点,
为极点, 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线 的极坐标方程为
的极坐标方程为 ,求直线
,求直线