网址:http://m.1010jiajiao.com/timu_id_77456[举报]
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点
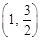 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)是否存过点 (2,1)的直线
(2,1)的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【解析】第一问利用设椭圆 的方程为
的方程为 ,由题意得
,由题意得
解得
第二问若存在直线 满足条件的方程为
满足条件的方程为 ,代入椭圆
,代入椭圆 的方程得
的方程得
 .
.
因为直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,设
,设 两点的坐标分别为
两点的坐标分别为 ,
,
所以
所以 .解得。
.解得。
解:⑴设椭圆 的方程为
的方程为 ,由题意得
,由题意得
解得 ,故椭圆
,故椭圆 的方程为
的方程为 .……………………4分
.……………………4分
⑵若存在直线 满足条件的方程为
满足条件的方程为 ,代入椭圆
,代入椭圆 的方程得
的方程得
 .
.
因为直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,设
,设 两点的坐标分别为
两点的坐标分别为 ,
,
所以
所以 .
.
又 ,
,
因为 ,即
,即 ,
,
所以
 .
.
即 .
.
所以 ,解得
,解得 .
.
因为A,B为不同的两点,所以k=1/2.
于是存在直线L1满足条件,其方程为y=1/2x
查看习题详情和答案>>
2.A解析:由![]() 知函数在
知函数在![]() 上有零点,又因为函数在(0,+
上有零点,又因为函数在(0,+![]() )上是减函数,所以函数y=f(x) 在(0,+
)上是减函数,所以函数y=f(x) 在(0,+![]() )上有且只有一个零点不妨设为
)上有且只有一个零点不妨设为![]() ,则
,则![]() ,又因为函数是偶函数,所以
,又因为函数是偶函数,所以![]() =0并且函数在(0,+
=0并且函数在(0,+![]() )上是减函数,因此-
)上是减函数,因此-![]() 是(-
是(-![]() ,0)上的唯一零点,所以函数共有两个零点
,0)上的唯一零点,所以函数共有两个零点
下列叙述中,是随机变量的有( )
①某工厂加工的零件,实际尺寸与规定尺寸之差;②标准状态下,水沸腾的温度;③某大桥一天经过的车辆数;④向平面上投掷一点,此点坐标.
A.②③ B.①② C.①③④ D.①③
查看习题详情和答案>>阅读下面的文言文,完成下面5题。
李斯论 (清)姚鼐
苏子瞻谓李斯以荀卿之学乱天下,是不然。秦之乱天下之法,无待于李斯,斯亦未尝以其学事秦。
|
君子之仕也,进不隐贤;小人之仕也,无论所学识非也,即有学识甚当,见其君国行事,悖谬无义,疾首嚬蹙于私家之居,而矜夸导誉于朝庭之上,知其不义而劝为之者,谓天下将谅我之无可奈何于吾君,而不吾罪也;知其将丧国家而为之者,谓当吾身容可以免也。且夫小人虽明知世之将乱,而终不以易目前之富贵,而以富贵之谋,贻天下之乱,固有终身安享荣乐,祸遗后人,而彼宴然①无与者矣。嗟乎!秦未亡而斯先被五刑夷三族也,其天之诛恶人,亦有时而信也邪!
且夫人有为善而受教于人者矣,未闻为恶而必受教于人者也。荀卿述先王而颂言儒效,虽间有得失,而大体得治世之要。而苏氏以李斯之害天下罪及于卿,不亦远乎?行其学而害秦者,商鞅也;舍其学而害秦者,李斯也。商君禁游宦,而李斯谏逐客②,其始之不同术也,而卒出于同者,岂其本志哉!宋之世,王介甫以平生所学,建熙宁新法,其后章惇、曾布、张商英、蔡京之伦,曷尝学介甫之学耶?而以介甫之政促亡宋,与李斯事颇相类。夫世言法术之学足亡人国,固也。吾谓人臣善探其君之隐,一以委曲变化从世好者,其为人尤可畏哉!尤可畏哉!
[注释]①宴然:安闲的样子。②谏逐客:秦始皇曾发布逐客令,驱逐六国来到秦国做官的人,李斯写了著名的《谏逐客书》,提出了反对意见。
对下列句子中加点的词语的解释,不正确的一项是( )
A.非是不足以中侈君张吾之宠 中:符合
B.灭三代法而尚督责 尚:崇尚
C.知其不义而劝为之者 劝:鼓励
D.而终不以易目前之富贵 易:交换
下列各组句子中,加点的词的意义和用法相同的一组是( )
A.因秦国地形便利 不如因普遇之
B.设所遭值非始皇、二世 非其身之所种则不食
C.且夫小人虽明知世之将乱 臣死且不避,卮酒安足辞
D.不亦远乎 王之好乐甚,则齐国其庶几乎
下列各项中,加点词语与现代汉语意义不相同的一项是( )
A.小人之仕也,无论所学识非也
B.而大体得治世之要
C.而以富贵之谋,贻天下之乱
D.一以委曲变化从世好者
下列各句中对文章的阐述,不正确的一项是( )
A.苏轼认为李斯以荀卿之学辅佐秦朝行暴政,致使天下大乱,作者则认为李斯是完全舍弃了荀子的说学,李斯的做法只不过是追随时势罢了。
B.作者由论李斯事秦进而泛论人臣事君的问题,强调为臣者对于国君的“悖谬无义”之政,不应为自身的富贵而阿附甚至助长之。
C.此文主旨在于指出秦行暴政是君王自身的原因,作者所论的不可“趋时”,“中侈君张吾之宠”的道理,在今天仍有借鉴意义。
D.文章开门见山,摆出苏轼的观点,然后通过对秦国发展历史的分析,驳斥了苏说的谬论,提出了自己的见解。论证严密,逐层深入,是一篇典范的史论。
把文言文阅读材料中画横线的句子翻译成现代汉语。
(1)秦之甘于刻薄而便于严法久矣
译文:
(2)谓天下将谅我之无可奈何于吾君,而不吾罪也
译文:
(3)其始之不同术也,而卒出于同者,岂其本志哉
译文:
查看习题详情和答案>>已知数列 的前
的前 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求 的通项公式;
的通项公式;
(Ⅱ) 设 (
( N*).
N*).
①证明:  ;
;
② 求证: .
.
【解析】本试题主要考查了数列的通项公式的求解和运用。运用 关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到
关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到 ,②由于
,②由于 ,
,
所以 利用放缩法,从此得到结论。
利用放缩法,从此得到结论。
解:(Ⅰ)当 时,由
时,由 得
得 . ……2分
. ……2分
若存在 由
由 得
得 ,
,
从而有 ,与
,与 矛盾,所以
矛盾,所以 .
.
从而由 得
得 得
得 . ……6分
. ……6分
(Ⅱ)①证明:
证法一:∵ ∴
∴
∴
∴ .…………10分
.…………10分
证法二: ,下同证法一.
……10分
,下同证法一.
……10分
证法三:(利用对偶式)设 ,
, ,
,
则 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因为
,又因为 ,所以
,所以 .即
.即
 ………10分
………10分
证法四:(数学归纳法)①当 时,
时,  ,命题成立;
,命题成立;
②假设 时,命题成立,即
时,命题成立,即 ,
,
则当 时,
时,

 即
即
即
故当 时,命题成立.
时,命题成立.
综上可知,对一切非零自然数 ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于 ,
,
所以 ,
,
从而 .
.
也即
查看习题详情和答案>>
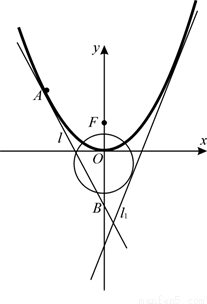
如图,已知直线 (
(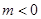 )与抛物线
)与抛物线 :
: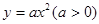 和圆
和圆 :
: 都相切,
都相切, 是
是 的焦点.
的焦点.
(Ⅰ)求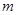 与
与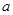 的值;
的值;
(Ⅱ)设 是
是 上的一动点,以
上的一动点,以 为切点作抛物线
为切点作抛物线 的切线
的切线 ,直线
,直线 交
交 轴于点
轴于点 ,以
,以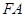 、
、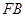 为邻边作平行四边形
为邻边作平行四边形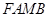 ,证明:点
,证明:点 在一条定直线上;
在一条定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点 所在的定直线为
所在的定直线为 , 直线
, 直线 与
与 轴交点为
轴交点为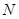 ,连接
,连接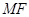 交抛物线
交抛物线 于
于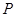 、
、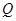 两点,求△
两点,求△ 的面积
的面积 的取值范围.
的取值范围.
【解析】第一问中利用圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去)
舍去)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
,
第二问中,由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形
, ∵四边形FAMB是以FA、FB为邻边作平行四边形
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线
第三问中,设直线 ,代入
,代入 得
得 结合韦达定理得到。
结合韦达定理得到。
解:(Ⅰ)由已知,圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去). …………………(2分)
舍去). …………………(2分)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
, .
……(2分)
.
……(2分)
(Ⅱ)由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形,
, ∵四边形FAMB是以FA、FB为邻边作平行四边形,
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线 上.…(2分)
上.…(2分)
(Ⅲ)设直线 ,代入
,代入 得
得 , ……)得
, ……)得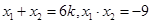 ,
…………………………… (2分)
,
…………………………… (2分)
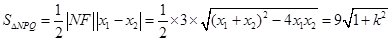 ,
,
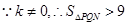 .
. △
△ 的面积
的面积 范围是
范围是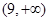
查看习题详情和答案>>