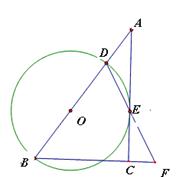
摘要：25．如下图.在△ABC中.∠C=90°.P为AB上一点.且点P不与点A重合.过P作PE⊥AB交AC边于点E.点E不与点C重合.若AB=10.AC=8.设AP的长为.四边形PECB周长为y.求y与的函数关系式.并写出自变量的取值范围．
网址：http://m.1010jiajiao.com/timu_id_772392[举报]
如下图，在△ABC中，∠C＝90°，AC＝6，BC＝8，M是BC的中点，P为AB上的一个动点，(可以与A、B重合)，并作∠MPD＝90°，PD交BC(或BC的延长线)于点D．
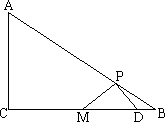
(1)记BP的长为x，△BPM的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围；
(2)是否存在这样的点P，使得△MPD与△ABC相似？若存在，请求出x的值；若不存在，请说明理由．
如图，在△ABC中，AC=AB=2，∠A=90°，将一块与△ABC全等的三角板的直角顶点放在点C上，一直角边与BC重叠．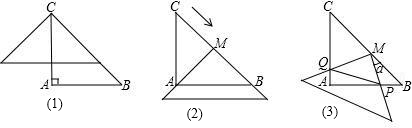
（1）操作1：固定△ABC，将三角板沿C?B方向平移，使其直角顶点落在BC的中点M，如图2示．探究：三角板沿C?B方向平移的距离为 ；
（2）操作2：在（1）情形下，将三角板绕BC的中点M顺时针方向旋转角度α（0°＜α＜90°）如图3示．探究：设三角板两直角边分别与AB、AC交于P、Q，观察四边形MPAQ形状的变化，发现其面积始终不变，那么四边形MPAQ的面积S四边形MPAQ= ；
（3）在（2）的情形下，连PQ，设BP=x，记△APQ的面积为y，试求y关于x的函数关系式；并求x为何值时，△PQA面积有最大值，最大值是多少？ 查看习题详情和答案>>
（1）操作1：固定△ABC，将三角板沿C?B方向平移，使其直角顶点落在BC的中点M，如图2示．探究：三角板沿C?B方向平移的距离为
（2）操作2：在（1）情形下，将三角板绕BC的中点M顺时针方向旋转角度α（0°＜α＜90°）如图3示．探究：设三角板两直角边分别与AB、AC交于P、Q，观察四边形MPAQ形状的变化，发现其面积始终不变，那么四边形MPAQ的面积S四边形MPAQ=
（3）在（2）的情形下，连PQ，设BP=x，记△APQ的面积为y，试求y关于x的函数关系式；并求x为何值时，△PQA面积有最大值，最大值是多少？ 查看习题详情和答案>>
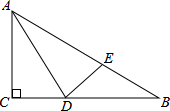如图，在△ABC中，∠C=90°，D是边BC上一点，且∠ADC=60°，那么下列说法中错误的是（ ）
如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠CAB交BC于点D，E为AB上一点，连接DE，则下列说法错误的是（ ）| A、∠CAD=30° | B、AD=BD | C、BD=2CD | D、CD=ED |
