摘要：13．一个矩形的长和宽分别为d.b.它的周长为14.面积为10.那么a2b+ab2的值为.
网址：http://m.1010jiajiao.com/timu_id_768443[举报]
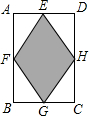由于矩形和菱形特殊的对称美和矩形的四个角都是直角，从而为密铺提供了方便，因此墙砖一般设计为矩形，而且图案以菱形居多，如图3所示，是长为30cm，宽为20cm的一块矩形瓷砖，E、F、G、H分别是矩形四边的中点，阴影部分为黄色，其它部分为淡蓝色，现有一面长为6m，高为3m的墙面准备贴这种瓷砖，那么：这面墙要贴的瓷砖数及全部贴满后这面墙上最多出现的与图3中面积相等的菱形个数分别为
- A.288、561
- B.300、561
- C.288、566
- D.300、566
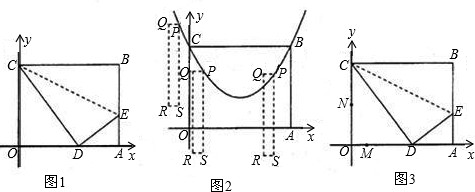
如图1，矩形OABC的顶点O为原点，点E在AB上，把△CBE沿CE折叠，使点B落在OA边上的点D处，点A、D坐标分别为（10，0）和（6，0），抛物线y=
x2+bx+c过点C、B．
（1）求C、B两点的坐标及该抛物线的解析式；
（2）如图2，长、宽一定的矩形PQRS的宽PQ=1，点P沿（1）中的抛物线滑动，在滑动过程中PQ∥x轴，且RS在PQ的下方，当P点横坐标为-1时，点S距离x轴
个单位，当矩形PQRS在滑动过程中被x轴分成上下两部分的面积比为2：3时，求点P的坐标；
（3）如图3，动点M、N同时从点O出发，点M以每秒3个单位长度的速度沿折线ODC按O→D→C的路线运动，点N以每秒8个单位长度的速度沿折线OCD按O?C?D的路线运动，当M、N两点相遇时，它们都停止运动．设M、N同时从点O出发t秒时，△OMN的面积为S．①求出S与t的函数关系式，并写出t的取值范围：②设S0是①中函数S的最大值，那么S0= ．
查看习题详情和答案>>
| 1 |
| 5 |
（1）求C、B两点的坐标及该抛物线的解析式；
（2）如图2，长、宽一定的矩形PQRS的宽PQ=1，点P沿（1）中的抛物线滑动，在滑动过程中PQ∥x轴，且RS在PQ的下方，当P点横坐标为-1时，点S距离x轴
| 11 |
| 5 |
（3）如图3，动点M、N同时从点O出发，点M以每秒3个单位长度的速度沿折线ODC按O→D→C的路线运动，点N以每秒8个单位长度的速度沿折线OCD按O?C?D的路线运动，当M、N两点相遇时，它们都停止运动．设M、N同时从点O出发t秒时，△OMN的面积为S．①求出S与t的函数关系式，并写出t的取值范围：②设S0是①中函数S的最大值，那么S0=
查看习题详情和答案>>