摘要:(4)设直线与y轴交于点C与轴交于点D.求点C与点D的坐标,(5)求△AOB的面积.
网址:http://m.1010jiajiao.com/timu_id_766388[举报]
直线![]() 与
与![]() 轴交于
轴交于![]() 点,点
点,点![]() 在第一象限,且
在第一象限,且![]() ,
,![]() .
.
(1)若点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,求过
轴的对称点,求过![]() 三点的抛物线的表达式.
三点的抛物线的表达式.
(2)在(1)中的抛物线上是否存在点![]() (
(![]() 点在第一象限),使得以点
点在第一象限),使得以点![]() 为顶点的四边形是梯形?若存在,求出点
为顶点的四边形是梯形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若将点![]() 分别变换为点
分别变换为点![]() (
(![]() 且为常数),设过
且为常数),设过![]() 两点且以
两点且以![]() 的垂直平分线为对称轴的抛物线(开口向上)与
的垂直平分线为对称轴的抛物线(开口向上)与![]() 轴的交点为
轴的交点为![]() ,其顶点为
,其顶点为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,连结
,连结![]() ,抛物线
,抛物线![]() 从点
从点![]() 沿
沿![]() 方向平移,与直线
方向平移,与直线![]() 交于点
交于点![]() ,顶点
,顶点![]() 到
到![]() 点时停止移动.
点时停止移动.
(1)求线段![]() 所在直线的函数解析式;(2)设抛物线顶点
所在直线的函数解析式;(2)设抛物线顶点![]() 的横坐标为
的横坐标为![]() ,①用
,①用![]() 的代数式表示点
的代数式表示点![]() 的坐标;②当
的坐标;②当![]() 为何值时,线段
为何值时,线段![]() 最短;
最短;
(3)当线段![]() 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点![]() ,使△
,使△![]() 的面积与△
的面积与△![]() 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点![]() 的坐标;若,不存在,请说明理由.
的坐标;若,不存在,请说明理由.

直线 与坐标轴分别交于A、B两点,OA、OB的长分别是方程
与坐标轴分别交于A、B两点,OA、OB的长分别是方程 的两根(
的两根( ),动点P从O点出发,沿路线P→B→A以每秒1个单位长度的速度运动,到达A点时运动停止.
),动点P从O点出发,沿路线P→B→A以每秒1个单位长度的速度运动,到达A点时运动停止.
(1)直接写出A、B两点的坐标;
(2)设点P的运动时间为t(秒),△OPA的面积为S,求S与t之间的函数关系式(不必写出自变量的取值范围);
(3)当S=12时,直接写出点P的坐标,此时,在坐标轴上是否存在点M,使以O、A、P、M为顶点的四边形是梯形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
 与坐标轴分别交于A、B两点,OA、OB的长分别是方程
与坐标轴分别交于A、B两点,OA、OB的长分别是方程 的两根(
的两根( ),动点P从O点出发,沿路线P→B→A以每秒1个单位长度的速度运动,到达A点时运动停止.
),动点P从O点出发,沿路线P→B→A以每秒1个单位长度的速度运动,到达A点时运动停止. (1)直接写出A、B两点的坐标;
(2)设点P的运动时间为t(秒),△OPA的面积为S,求S与t之间的函数关系式(不必写出自变量的取值范围);
(3)当S=12时,直接写出点P的坐标,此时,在坐标轴上是否存在点M,使以O、A、P、M为顶点的四边形是梯形?若存在,请直接写出点M的坐标;若不存在,请说明理由.


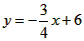 与坐标轴分别交于A,B两点,动点P、Q同时从O点出发,同时到达A点,运动停止。点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动。
与坐标轴分别交于A,B两点,动点P、Q同时从O点出发,同时到达A点,运动停止。点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动。