摘要：18． 如图.已知△ABC是等边三角形.D.E分别在边BC.AC上.且CD=CE.连结DE并延长至点F.使EF=AE.连结AF.BE和CF．(1)请在图中找出一对全等三角形.用符号“≌ 表示.并加以证明．(2)判断四边形ABDF是怎样的四边形.并说明理由．(3)若AB=6.BD=2DC.求四边形ABEF的面积．
网址：http://m.1010jiajiao.com/timu_id_766302[举报]
（本题满分12分，任选一题作答．）
Ⅰ、如图①，在平面直角坐标系中，O为坐标原点，边长为5的正三角形OAB的OA边在x轴的正半轴上．点C、D同时从点O出发，点C以1单位长/秒的速度向点A运动，点D以2个单位长/秒的速度沿折线OBA运动．设运动时间为t秒，0＜t＜5．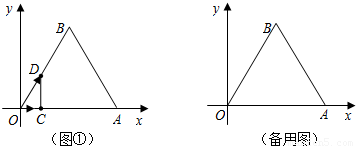
（1）当
时，证明DC⊥OA；
（2）若△OCD的面积为S，求S与t的函数关系式；
（3）以点C为中心，将CD所在的直线顺时针旋转60°交AB边于点E，若以O、C、E、D为顶点的四边形是梯形，求点E的坐标．
Ⅱ、（1）如图Ⅱ-1，已知△ABC，过点A画一条平分三角形面积的直线；
（2）如图Ⅱ-2，已知l1∥l2，点E，F在l1上，点G，H在l2上，试说明△EGO与△FHO面积相等．
（3）如图Ⅱ-3，点M在△ABC的边上，过点M画一条平分三角形面积的直线．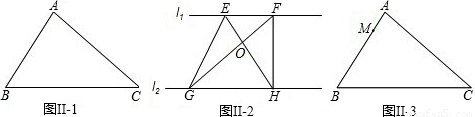
查看习题详情和答案>>
Ⅰ、如图①，在平面直角坐标系中，O为坐标原点，边长为5的正三角形OAB的OA边在x轴的正半轴上．点C、D同时从点O出发，点C以1单位长/秒的速度向点A运动，点D以2个单位长/秒的速度沿折线OBA运动．设运动时间为t秒，0＜t＜5．
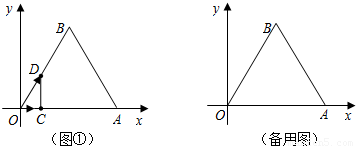
（1）当
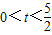时，证明DC⊥OA；（2）若△OCD的面积为S，求S与t的函数关系式；
（3）以点C为中心，将CD所在的直线顺时针旋转60°交AB边于点E，若以O、C、E、D为顶点的四边形是梯形，求点E的坐标．
Ⅱ、（1）如图Ⅱ-1，已知△ABC，过点A画一条平分三角形面积的直线；
（2）如图Ⅱ-2，已知l1∥l2，点E，F在l1上，点G，H在l2上，试说明△EGO与△FHO面积相等．
（3）如图Ⅱ-3，点M在△ABC的边上，过点M画一条平分三角形面积的直线．
查看习题详情和答案>>
（本小题满分8分）
已知，在△ABC中，∠BAC=90°，AB=AC，BC=
，点D、E在BC边上（均不与点B、C重合，点D始终在点E左侧），且∠DAE＝45°．
1.（1）请在图①中找出两对相似但不全等的三角形，写在横线上 ， ；
2.（2）设BE＝m，CD＝n，求m与n的函数关系式，并写出自变量n的取值范围；
3.（3）如图②，当BE＝CD时，求DE的长；
4.（4）求证：无论BE与CD是否相等，都有DE2=BD2+CE2.
查看习题详情和答案>>
（本小题满分10分）已知，等腰Rt△ABC中，点O是斜边的中点，△MPN是直角三角形，固定△ABC，滑动△MPN，在滑动过程中始终保持点P在AC上，且 PM⊥AB，PN⊥BC，垂足分别为E、F．
（1）如图1，当点P与点O重合时，OE、OF的数量和位置关系分别是____ __．
（2）当△MPN移动到图2的位置时，（1）中的结论还成立吗？请说明理由．
（3）如图3，等腰Rt△ABC的腰长为6，点P在AC的延长线上时，Rt△MPN的边PM
与AB的延长线交于点E，直线BC与直线NP交于点F，OE交BC于点H，且 EH： HO=2：5，则BE的长是多少？
查看习题详情和答案>>
