摘要:13.如图.⊙O与△ABC中AB.AC的延长线及BC边相切.且∠ACB=90°.∠A.∠B.∠C所对的边长依次为3.4.5.则⊙O的半径是
网址:http://m.1010jiajiao.com/timu_id_765079[举报]
 如图,在△ABC中,AB>AC,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.
如图,在△ABC中,AB>AC,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.(1)请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),
使△BDE≌△CDF,并给出证明.你添加的条件是:
BD=DC(或D是BC的中点,FD=ED,CF=BE)
BD=DC(或D是BC的中点,FD=ED,CF=BE)
;(2)在(1)的条件下,连接CE、BF,判断CE与BF的数量关系与位置关系,并说明理由.
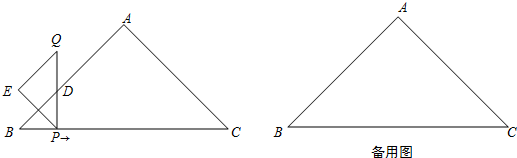
如图,在Rt△ABC中,AB=AC=4
.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
(1)在整个运动过程中,设△ABC与△PQE重叠部分的面积为S,请直接写出S与t之间的函数关系式以及相应的自变量t的取值范围;
(2)当点D在线段AB上时,连接AQ、AP,是否存在这样的t,使得△APQ成为等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由;
(3)当t=4秒时,以PQ为斜边在PQ右侧作等腰直角三角形PQF,将四边形PEQF绕点P旋转,PE与线段AB相交于点M,PF与线段AC相交于点N.试判断在这一旋转过程中,四边形PMAN的面积是否发生变化?若发生变化,求出四边形PMAN的面积y与PM的长x之间的函数关系式以及相应的自变量x的取值范围;若不发生变化,求出此定值.
查看习题详情和答案>>
| 2 |
(1)在整个运动过程中,设△ABC与△PQE重叠部分的面积为S,请直接写出S与t之间的函数关系式以及相应的自变量t的取值范围;
(2)当点D在线段AB上时,连接AQ、AP,是否存在这样的t,使得△APQ成为等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由;
(3)当t=4秒时,以PQ为斜边在PQ右侧作等腰直角三角形PQF,将四边形PEQF绕点P旋转,PE与线段AB相交于点M,PF与线段AC相交于点N.试判断在这一旋转过程中,四边形PMAN的面积是否发生变化?若发生变化,求出四边形PMAN的面积y与PM的长x之间的函数关系式以及相应的自变量x的取值范围;若不发生变化,求出此定值.

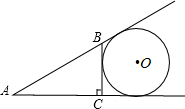 如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是________.
如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是________. (2009•自贡)如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是
(2009•自贡)如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是