摘要:(2)当点旋转到图2或图3中的位置时.与有何数量关系?请分别写出猜想.并任选一种情况证明.
网址:http://m.1010jiajiao.com/timu_id_762533[举报]
已知:在![]() 中,
中,![]() ,动点
,动点![]() 绕
绕![]() 的顶点
的顶点![]() 逆时针旋转,且
逆时针旋转,且![]() ,连结
,连结![]() .过
.过![]() 、
、![]() 的中点
的中点![]() 、
、![]() 作直线,直线
作直线,直线![]() 与直线
与直线![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() .
.
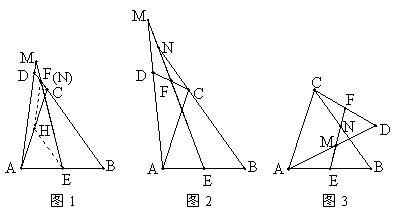
(1)如图1,当点![]() 旋转到
旋转到![]() 的延长线上时,点
的延长线上时,点![]() 恰好与点
恰好与点![]() 重合,取
重合,取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,根据三角形中位线定理和平行线的性质,可得结论
,根据三角形中位线定理和平行线的性质,可得结论![]() (不需证明).
(不需证明).
(2)当点![]() 旋转到图2或图3中的位置时,
旋转到图2或图3中的位置时,![]() 与
与![]() 有何数量关系?请分别写出猜想,并任选一种情况证明.
有何数量关系?请分别写出猜想,并任选一种情况证明.
如图,在三个等圆两两外切,且与正中位置的小圆相外切,旋转指针,任其自由停止,当指针停在某个圆面上时, 得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).
得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).
(1)“转动一次,得到的数字恰好是0”的概率是
;
(2)用树状图或列表法,求“转动两次,前后两次得到的数字的绝对值相等”的概率.
查看习题详情和答案>>
 得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).
得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).(1)“转动一次,得到的数字恰好是0”的概率是
| 1 |
| 3 |
| 1 |
| 3 |
(2)用树状图或列表法,求“转动两次,前后两次得到的数字的绝对值相等”的概率.
如图,在三个等圆两两外切,且与正中位置的小圆相外切,旋转指针,任其自由停止,当指针停在某个圆面上时,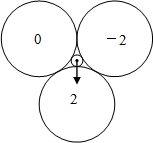 得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).
得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).
(1)“转动一次,得到的数字恰好是0”的概率是______;
(2)用树状图或列表法,求“转动两次,前后两次得到的数字的绝对值相等”的概率.
查看习题详情和答案>>
如图,在三个等圆两两外切,且与正中位置的小圆相外切,旋转指针,任其自由停止,当指针停在某个圆面上时,得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).
(1)“转动一次,得到的数字恰好是0”的概率是______;
(2)用树状图或列表法,求“转动两次,前后两次得到的数字的绝对值相等”的概率.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)“转动一次,得到的数字恰好是0”的概率是______;
(2)用树状图或列表法,求“转动两次,前后两次得到的数字的绝对值相等”的概率.
 查看习题详情和答案>>
查看习题详情和答案>>
| 已知:在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连结DC.过AB、DC的中点E、F作直线,直线EF与直线AD、BC分别相交于点M、N. |
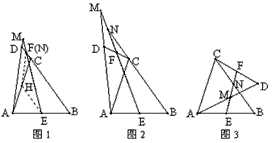 |
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连结HE、HF,根据三角形中位线定理和平行线的性质,可得结论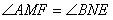 (不需证明). (不需证明).(2)当点D旋转到图2或图3中的位置时, 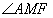 与 与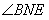 有何数量关系?请分别写出猜想,并任选一种情况证明. 有何数量关系?请分别写出猜想,并任选一种情况证明. |