题目内容
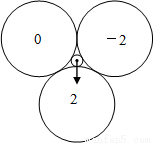
如图,在三个等圆两两外切,且与正中位置的小圆相外切,旋转指针,任其自由停止,当指针停在某个圆面上时,得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).(1)“转动一次,得到的数字恰好是0”的概率是______;
(2)用树状图或列表法,求“转动两次,前后两次得到的数字的绝对值相等”的概率.
【答案】分析:(1)由于三个等圆两两外切,并且与正中位置的小圆相外切,则指针在每个圆面上旋转的角度都为120°,则转动一次,得到的数字恰好是0”的概率=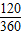 ;
;
(2)画树状图展示所有9种等可能的结果数,其中前后两次得到的数字的绝对值相等有5种可能,然后根据概率的定义计算即可.
解答:解:(1) ;
;
(2)画树状图:
共有9种等可能的结果数,其中前后两次得到的数字的绝对值相等有5种可能,
所以转动两次,前后两次得到的数字的绝对值相等”的概率= .
.
点评:本题考查了列表法与树状图法:先通过列表法或树状图法展示所有等可能的结果数n,再找出其中某事件所占有的结果数m,然后根据概率的定义计算这个事件的概率=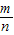 .
.
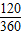 ;
;(2)画树状图展示所有9种等可能的结果数,其中前后两次得到的数字的绝对值相等有5种可能,然后根据概率的定义计算即可.
解答:解:(1)
 ;
;(2)画树状图:

共有9种等可能的结果数,其中前后两次得到的数字的绝对值相等有5种可能,
所以转动两次,前后两次得到的数字的绝对值相等”的概率=
 .
.点评:本题考查了列表法与树状图法:先通过列表法或树状图法展示所有等可能的结果数n,再找出其中某事件所占有的结果数m,然后根据概率的定义计算这个事件的概率=
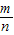 .
. 
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
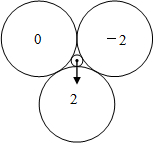 得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).
得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).

 得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).
得到相应圆面上的一个数字(当指针恰好指向两等圆切点时,当作指向右侧的圆面).