摘要:24.定义为函数的 “特征数 .如:函数的“特征数 是.函数的“特征数 是,函数的“特征数 是
网址:http://m.1010jiajiao.com/timu_id_762472[举报]
定义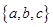 为函数
为函数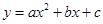 的“特征数”.如:函数
的“特征数”.如:函数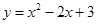 的“特征数”是
的“特征数”是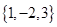 ,函数
,函数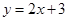 的“特征数”是
的“特征数”是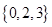 ,函数
,函数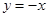 的“特征数”是
的“特征数”是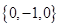

(1)将“特征数”是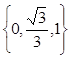 的函数图象向下平移2个单位,得到一个新函数,这个新
的函数图象向下平移2个单位,得到一个新函数,这个新
函数的解析式是 ;
(2)在(1)中,平移前后的两个函数分别与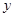 轴交于A、B两点,与直线
轴交于A、B两点,与直线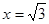 分别交于
分别交于
D、C两点,在给出的平面直角坐标系中画出图形,判断以A、B、C、D四点为顶点的四边形形状,并说明理由;
(3)若(2)中的四边形与“特征数”是的函数图象有交点,试求出实数
b 的取值范围.
定义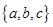 为函数
为函数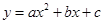 的“特征数”.如:函数
的“特征数”.如:函数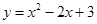 的“特征数”是
的“特征数”是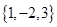 ,函数
,函数 的“特征数”是
的“特征数”是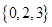 ,函数
,函数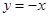 的“特征数”是
的“特征数”是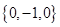
(1)将“特征数”是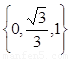 的函数图象向下平移2个单位,得到一个新函数,这个新
的函数图象向下平移2个单位,得到一个新函数,这个新
函数的解析式是 ;
(2)在(1)中,平移前后的两个函数分别与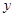 轴交于A、B两点,与直线
轴交于A、B两点,与直线 分别交于
分别交于
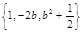 D、C两点,在给出的平面直角坐标系中画出图形,判断以A、B、C、D四点为顶点的四边形形状,并说明理由;
D、C两点,在给出的平面直角坐标系中画出图形,判断以A、B、C、D四点为顶点的四边形形状,并说明理由;
(3)若(2)中的四边形与“特征数”是的函数图象有交点,试求出实数
b 的取值范围.
查看习题详情和答案>>
定义![]() 为函数
为函数![]() 的 “特征数”.如:函数
的 “特征数”.如:函数![]() 的“特征数”是
的“特征数”是![]() ,函数
,函数![]() 的“特征数”是
的“特征数”是![]() .
.
(1)将“特征数”是![]() 的函数的图象向下平移2个单位,得到一个新函数图象,求这
的函数的图象向下平移2个单位,得到一个新函数图象,求这![]() 个新函数图象的解析式;
个新函数图象的解析式;
(2)“特征数”是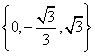 的函数图象与x、y轴分别交点C、D, “特征数”是
的函数图象与x、y轴分别交点C、D, “特征数”是![]() 的函数图象与x轴交于点E, 点O是原点, 判断△ODC与△OED是否相似,请说明理由.
的函数图象与x轴交于点E, 点O是原点, 判断△ODC与△OED是否相似,请说明理由.
 定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}(1)将“特征数”是{0,
| ||
| 3 |
| ||
| 3 |
(2)在(1)中,平移前后的两个函数分别与y轴交于A、B两点,与直线x=
| 3 |
(3)若(2)中的四边形与“特征数”是{1,-2b,b2+
| 1 |
| 2 |
 定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}