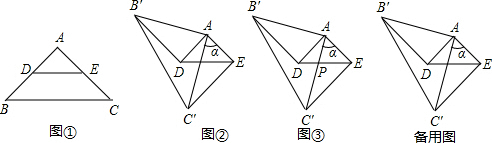
(2)设图2中的延长线交于.并将图2中的△在线段上沿着方向以每秒1个单位的速度平移.平移后的△设为△．设△移动(点在线段上)的时间为x秒.若△与△重叠部分的面积为y.求y与x之间的函数解析式.并写出自——青夏教育精英家教网——

摘要：(2)设图2中的延长线交于.并将图2中的△在线段上沿着方向以每秒1个单位的速度平移.平移后的△设为△．设△移动(点在线段上)的时间为x秒.若△与△重叠部分的面积为y.求y与x之间的函数解析式.并写出自变量x的取值范围,

网址：http://m.1010jiajiao.com/timu_id_760531[举报]

如图1，已知Rt△ABC的直角边AC的长为2，以AC为直径的⊙O与斜边AB交于点D，过D点作⊙O的切线

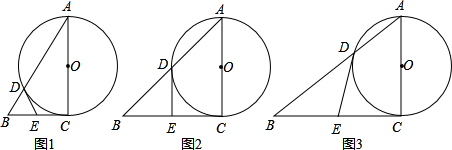
（1）求证：BE=DE；
（2）延长DE与AC的延长线交于点F，若DF=

，求△ABC的面积；
（3）从图1中，显然可知BC＜AC．试分别讨论在其它条件不变，当BC=AC（图2）和BC＞AC（图3）时，直线DE与直线AC还会相交吗？若不能相交，请简要说明理由；若能相交，设交点为F'且DF'=

，请再求出△ABC的面积．查看习题详情和答案>>

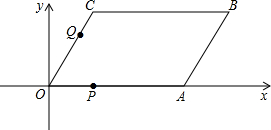（2013•安阳一模）如图，在?ABCD中，点A在x轴上，∠AOC=60°，OC=4cm，OA=8cm，动点P从点O出发，以1cm/s的速度沿线段OA运动；动点Q同时从点O出发，以a cm/s的速度沿线段OC→CB运动，其中一点先到达终点，另一点也随着停止运动．设运动时间为t
（1）填空：点C的坐标是

，对角线OB的长度是

cm．
（2）当a=1时，设△OPQ面积为S，求S与t的函数关系式，并直接写出当t为何值时，S的最大值？
（3）设线段PQ与对角线OB交于一点M，当a=

，t=7时，以O、M、P为顶点的三角形是否与△OAB相似？请说明理由．

查看习题详情和答案>>

如图，在平行四边形ABCD中，AB在x轴上，D点y轴上，∠C=60°，BC=6，B点坐标为（4，0）．点M是边AD上一点，且DM：AD=1：3．点E、F分别从A、C同时出发，以1厘米/秒的速度分别沿AB、CB向点B运动（当点F运动到点B时，点E随之停止运动），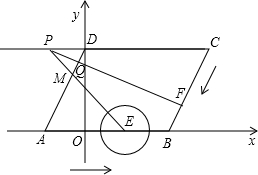

EM、CD的延长线交于点P，FP交AD于点Q．⊙E半径为

，设运动时间为x秒．
（1）求直线BC的解析式；
（2）当x为何值时，PF⊥AD；
（3）在（2）问条件下，⊙E与直线PF是否相切？如果相切，加以证明，并求出切点的坐标；如果不相切，说明理由．查看习题详情和答案>>

如图，在平面直角坐标系中，矩形OABC的顶点A（0，3），C（-1，0），将矩形OABC绕原点O顺时

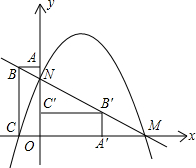针方向旋转90度，得矩形OA′B′C′矩形设直线BB’与x轴交于点M，与y轴交于点N，抛物线经过点C，M，N点．
解答下列问题：
（1）设直线BB′表示的函数解析式为y=mx+n，求m，n；
（2）求抛物线表示的二次函数的解析式；
（3）在抛物线上求出使S_△PB′C′=S_矩形OABC的所有点P的坐标．查看习题详情和答案>>

如图①，在△ABC中，AB=AC，∠BAC=90°，D、E分别是AB、AC边的中点．将△ABC绕点A顺时针旋转α角（0°＜α＜180°），得到△AB′C′（如图②）．
（1）探究DB′与EC′的数量关系，并给予证明；
（2）当DB′∥AE时，求此时旋转角α的度数；
（3）如图③，在旋转过程中，设 AC′与DE所在直线交于点P，当△ADP成为等腰三角形时，求此时的旋转角α的度数．（直接写出结果）

查看习题详情和答案>>