摘要:(2)设.梯形的面积为.求与之间的函数关系式,当点运动到什么位置时.四边形面积最大.并求出最大面积,
网址:http://m.1010jiajiao.com/timu_id_760245[举报]
(本题满分12分)正方形![]() 边长为4,
边长为4,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的两个动点,当
上的两个动点,当![]() 点在
点在![]() 上运动时,保持
上运动时,保持![]() 和
和![]() 垂直,
垂直,

1.⑴证明:![]() ;
;
2.⑵设![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
3.⑶梯形![]() 的面积可能等于12吗?为什么?
的面积可能等于12吗?为什么?
查看习题详情和答案>>
正方形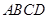 的边长为4,
的边长为4,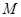 、
、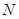 分别是
分别是 、
、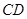 上的两个动点,当
上的两个动点,当 点在
点在 上运动时,始终保持
上运动时,始终保持 和
和 垂直,
垂直,
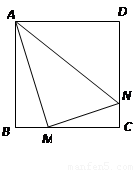
(1)证明: ;
;
(2)设 ,梯形
,梯形 的面积为
的面积为 ,求
,求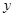 与
与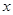 之间的函数关系式;当
之间的函数关系式;当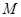 点运动到什么位置时,四边形
点运动到什么位置时,四边形 面积最大,并求出最大面积;
面积最大,并求出最大面积;
(3)当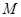 点运动到什么位置时,
点运动到什么位置时, ?并求出此时BM的长.
?并求出此时BM的长.
查看习题详情和答案>>
如图,在等腰梯形 中,
中,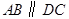 ,
,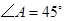 ,
,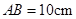 ,
,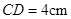 .等腰直角三角形
.等腰直角三角形 的斜边
的斜边 ,
,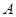 点与
点与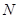 点重合,
点重合,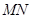 和
和 在一条直线上,设等腰梯形
在一条直线上,设等腰梯形 不动,等腰直角三角形
不动,等腰直角三角形 沿
沿 所在直线以
所在直线以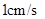 的速度向右移动,直到点
的速度向右移动,直到点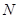 与点
与点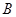 重合为止.
重合为止.
(1)等腰直角三角形 在整个移动过程中与等腰梯形
在整个移动过程中与等腰梯形 重叠部分的形状由 形
重叠部分的形状由 形
变化为 形;
(2)设当等腰直角三角形 移动
移动 时,等腰直角三角形
时,等腰直角三角形 与等腰梯形
与等腰梯形 重
重
叠部分的面积为 ,求
,求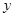 与
与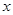 之间的函数关系式;
之间的函数关系式;
(3)当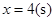 时,求等腰直角三角形
时,求等腰直角三角形 与等腰梯形
与等腰梯形 重叠部分的面积.
重叠部分的面积.
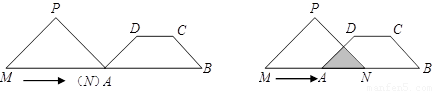
查看习题详情和答案>>
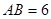 ,
,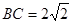 ,
,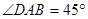 ,以
,以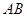 所在直线为
所在直线为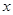 轴,
轴, 为坐标原点,建立直角坐标系,将等腰梯形ABCD绕A点按顺时针方向旋转
为坐标原点,建立直角坐标系,将等腰梯形ABCD绕A点按顺时针方向旋转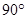 得到等腰梯形OEFG(O、E、F、G分别是A、B、C、D旋转后的对应点)(如图).
得到等腰梯形OEFG(O、E、F、G分别是A、B、C、D旋转后的对应点)(如图). 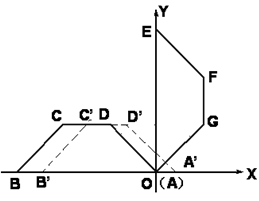
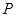 ,使
,使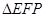 为等腰三角形,若存在,写出出
为等腰三角形,若存在,写出出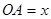 (0<x≤6),等腰梯形ABCD与等腰梯形OEFG重叠部分的面积为
(0<x≤6),等腰梯形ABCD与等腰梯形OEFG重叠部分的面积为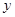 ,求
,求 中,
中, ,
, ,
,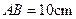 ,
, .等腰直角三角形
.等腰直角三角形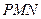 的斜边
的斜边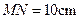 ,
,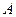 点与
点与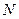 点重合,
点重合, 和
和 在一条直线上,设等腰梯形
在一条直线上,设等腰梯形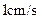 的速度向右移动,直到点
的速度向右移动,直到点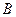 重合为止.
重合为止.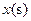 时,等腰直角三角形
时,等腰直角三角形 ,求
,求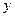 与
与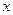 之间的函数关系式;
之间的函数关系式;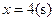 时,求等腰直角三角形
时,求等腰直角三角形