网址:http://m.1010jiajiao.com/timu_id_75896[举报]
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
D
A
B
D
B
C
B
C
D
B
1.提示:.files/image256.gif) 所以
所以.files/image258.gif) ,故选C。
,故选C。
2.提示:命题P:.files/image260.gif) ,所以命题P是假命题,
,所以命题P是假命题,
命题Q .files/image262.gif)
当.files/image264.gif) 时,。
时,。 .files/image266.gif) ,所以以命题Q是真命题,故选D。故选A。
,所以以命题Q是真命题,故选D。故选A。
3.提示:.files/image268.gif) 又
又.files/image270.gif) ,所以
,所以.files/image272.gif) ,故选D。
,故选D。
4.提示:在AB上取点D,使得.files/image274.gif) ,则点P只能在AD内运动,则
,则点P只能在AD内运动,则.files/image276.gif) ,
,
5.提示:.files/image278.gif) 故选B。
故选B。
6.提示:由图(1)改为图(2)后每次循环时.files/image280.gif) 的值都为1,因此运行过程出现无限循环,故选D
的值都为1,因此运行过程出现无限循环,故选D
7.提示:设全班40个人的总分为S,
则.files/image282.gif) ,故选B。
,故选B。
8.提示:.files/image284.gif)
所以约束条件为.files/image286.gif) 表示的平面区域是以点O(0,0),
表示的平面区域是以点O(0,0),.files/image050.gif) ,N(0,1),Q(2,3)为顶点的平行四边形(包括边界),故当
,N(0,1),Q(2,3)为顶点的平行四边形(包括边界),故当.files/image288.gif) 时,
时,.files/image290.gif) 的最大值是4,故选C。
的最大值是4,故选C。
.files/image291.gif) 9.提示:由
9.提示:由.files/image293.gif) 及
及.files/image295.gif) 得
得
.files/image297.gif) 如图
如图
过A作.files/image299.gif) 于M,则
于M,则
.files/image301.gif)
.files/image303.gif)
.files/image305.gif)
.files/image307.gif) 得
得.files/image309.gif) .
.
故选B.
10.提示:不妨设点(2,0)与曲线.files/image073.gif) 上不同的三的点距离为分别
上不同的三的点距离为分别.files/image311.gif) ,它们组成的等比数列的公比为
,它们组成的等比数列的公比为.files/image313.gif) 若令
若令.files/image315.gif) ,显然
,显然.files/image317.gif) ,又
,又.files/image319.gif) 所以
所以.files/image321.gif) ,
,.files/image323.gif) 不能取到
不能取到.files/image036.gif) 。故选B。
。故选B。
11.提示:使用特值法:取集合.files/image326.gif) 当
当.files/image328.gif) 可以排除A、B;
可以排除A、B;
取集合.files/image330.gif) ,当
,当.files/image332.gif) 可以排除C;故选D;
可以排除C;故选D;
12.提示:n棱柱有.files/image334.gif) 个顶点,被平面截去一个三棱锥后,可以分以下6种情形(图1~6)
个顶点,被平面截去一个三棱锥后,可以分以下6种情形(图1~6)
.files/image336.gif)
.files/image337.gif)
.files/image338.gif)
.files/image339.gif)
.files/image340.gif)
.files/image341.gif)
在图4,图6所示的情形,还剩.files/image334.gif) 个顶点;
个顶点;
在图5的情形,还剩.files/image343.gif) 个顶点;
个顶点;
在图2,图3的情形,还剩.files/image345.gif) 个顶点;
个顶点;
在图1的情形,还剩下.files/image347.gif) 个顶点.故选B.
个顶点.故选B.
二、填空题:
13..files/image349.gif)
提示:由.files/image351.gif)
14..files/image353.gif)
提示:斜率.files/image355.gif) ,切点
,切点.files/image357.gif) ,所以切线方程为:
,所以切线方程为:.files/image359.gif)
15..files/image361.gif)
提示:当.files/image363.gif) 时,不等式无解,当
时,不等式无解,当.files/image365.gif) 时,不等式变为
时,不等式变为.files/image367.gif) ,
,
由题意得.files/image369.gif) 或
或.files/image371.gif) ,所以,
,所以,.files/image373.gif) 或
或.files/image375.gif)
16..files/image377.gif)
三、解答题:
17.解:① ∵.files/image379.gif) ∴
∴.files/image381.gif) 的定义域为R;
的定义域为R;
② ∵.files/image383.gif) ,
,
∴.files/image185.gif) 为偶函数;
为偶函数;
③ ∵.files/image386.gif) , ∴
, ∴.files/image185.gif) 是周期为
是周期为.files/image389.gif) 的周期函数;
的周期函数;
④ 当.files/image391.gif) 时,
时,.files/image185.gif) =
=.files/image393.gif) ,
,
∴当.files/image391.gif) 时
时.files/image185.gif) 单调递减;当
单调递减;当.files/image397.gif) 时,
时,.files/image399.jpg)
.files/image185.gif) =
=.files/image401.gif) ,
,
.files/image185.gif) 单调递增;又∵
单调递增;又∵.files/image185.gif) 是周期为
是周期为.files/image389.gif) 的偶函数,∴
的偶函数,∴.files/image185.gif) 在
在.files/image406.gif) 上单调递增,在
上单调递增,在.files/image408.gif) 上单调递减(
上单调递减(.files/image410.gif) );
);
⑤ ∵当.files/image412.gif) 时
时.files/image414.gif) ;
;
当.files/image415.gif) 时
时.files/image417.gif) .∴
.∴.files/image185.gif) 的值域为
的值域为.files/image420.gif) ;
;
⑥由以上性质可得:.files/image185.gif) 在
在.files/image423.gif) 上的图象如图所示:
上的图象如图所示:
.files/image425.jpg)
18.解:(Ⅰ)取PC的中点G,连结EG,GD,则.files/image427.gif)
由(Ⅰ)知FD⊥平面PDC,.files/image429.gif) 面PDC,所以FD⊥DG。
面PDC,所以FD⊥DG。
所以四边形FEGD为矩形,因为G为等腰Rt△RPD斜边PC的中点,
所以DG⊥PC,
|
.files/image431.jpg)
.files/image433.gif)
.files/image435.gif) ;根据题意:
;根据题意:.files/image437.gif) 为
为.files/image439.gif) 的二个根;
的二个根;.files/image441.gif) ;
;.files/image443.gif) ;
;.files/image445.gif)
.files/image193.gif) ;
;.files/image447.gif) ;
;.files/image449.gif)
.files/image451.gif)
.files/image453.gif) ;
;.files/image455.gif)
.files/image457.gif)
.files/image459.gif) ;故:线段
;故:线段.files/image199.gif) 的中点
的中点.files/image201.gif) 在曲线
在曲线.files/image203.gif) 上;
上;.files/image461.gif) 。则
。则.files/image464.gif) 客人浏览景点数可能取值为0、1、2、3;相应在客人没有浏览的景点数的可能取值为3、2、1、0
客人浏览景点数可能取值为0、1、2、3;相应在客人没有浏览的景点数的可能取值为3、2、1、0.files/image466.gif)
.files/image468.gif)
.files/image470.gif)
.files/image205.gif) 的分布列为
的分布列为.files/image474.gif)
.files/image476.gif)
.files/image478.gif) 在
在.files/image480.gif) 上单调递增,那么要
上单调递增,那么要.files/image209.gif) 上单调递增,必须
上单调递增,必须.files/image484.gif) ,即
,即.files/image486.gif)
.files/image488.gif)
.files/image490.gif) 时,
时,.files/image492.gif)
.files/image494.gif) ,
,.files/image496.gif) 时,
时,.files/image215.gif) ,
,.files/image498.gif)
.files/image500.gif)
.files/image502.gif)
.files/image504.gif)
.files/image507.gif) 适合上式,
适合上式,.files/image509.gif)
.files/image512.gif) 时,
时,.files/image514.gif)
.files/image516.gif)
.files/image518.gif) ,则数列
,则数列.files/image211.gif) 是等差数列,首项为1,公差为1。
是等差数列,首项为1,公差为1。.files/image520.gif)
.files/image522.gif)
.files/image228.gif) 恒成立,
恒成立,.files/image525.gif) 恒成立,
恒成立,.files/image527.gif) 恒成立。
恒成立。.files/image219.gif) 为奇数时,即
为奇数时,即.files/image530.gif) 恒成立,又
恒成立,又.files/image532.gif) 的最小值为1,
的最小值为1,.files/image534.gif)
.files/image536.gif) 恒成立,又
恒成立,又.files/image538.gif) 的最大值为
的最大值为.files/image540.gif) ,
,.files/image542.gif)
.files/image544.gif) 又
又.files/image546.gif)
.files/image226.gif) 为整数,
为整数,.files/image549.gif) ,使得对任意
,使得对任意.files/image213.gif) ,都有
,都有.files/image552.gif)
.files/image554.gif) 则
则.files/image556.gif)
.files/image558.gif)
.files/image560.gif) 而
而.files/image235.gif) ,故
,故.files/image563.gif) ,
,.files/image243.gif) 在区间
在区间.files/image566.gif) 上单调递增。
上单调递增。.files/image568.gif) 得
得.files/image570.gif)
.files/image572.gif)
.files/image574.gif) 函数
函数.files/image577.gif) 时,
时,.files/image249.gif) 取得最小值,此时点F、G的坐标分别为
取得最小值,此时点F、G的坐标分别为.files/image580.gif)
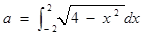 ,则
,则 展开式中的常数项为___________.
展开式中的常数项为___________.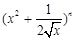 (
(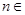 N*)展开式中,前三项的二项式系数和是
N*)展开式中,前三项的二项式系数和是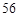 ,求:(Ⅰ)
,求:(Ⅰ)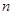 的值;(Ⅱ)展开式中的常数项.
的值;(Ⅱ)展开式中的常数项. ,则
,则 展开式中的常数项为
展开式中的常数项为