摘要:如图(20)图. 为平面.AB=5,A,B在棱l上的射影分别为A′.B′.AA′=3.BB′=2.若二面角的大小为.求: (Ⅰ)点B到平面的距离;(Ⅱ)异面直线l与AB所成的角.(21)小问5分. 如题是平面上的两点.动点P满足: (Ⅰ)求点P的轨迹方程;(Ⅱ)设d为点P到直线l: 的距离.若,求的值.(22)小问6分. 设各项均为正数的数列{an}满足. (Ⅰ)若求a3,a4,并猜想a2008的值;(Ⅱ)若对n≥2恒成立.求a2的值. 绝密★启用前2008年普通高等学校招生全国统一考试数学试题答案(1)C (2)A (3)C (4)A (5)D (6)D(7)B (8)C (9)B (10)B (11)A (12)C(13) |2 , 3| (14) -23 (15) -2 (16) 12 (1)已知{an}为等差数列.a2+a8=12,则a5等于(A)4 (B)5 (C)6 (D)7[答案]C[解析]本小题主要考查等差数列的性质.由得:.故选C.(2)设x是实数.则“x>0 是“|x|>0 的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既不充分也不必要条件[答案]A[解析]本小题主要考查充要条件的判定.由充分 而或.不必要.故选A. (3)曲线C:的普通方程为(A)(x-1)2+(y+1)2=1 (B) (x+1)2+(y+1)2=1(C) (x-1)2+(y-1)2=1 (D) (x-1)2+(y-1)2=1[答案]C[解析]本小题主要考查圆的参数方程.移项.平方相加..故选C.(4)若点P分有向线段所成的比为-.则点B分有向线段所成的比是(A)- (B)- (C) (D)3[答案]A[解析]本小题主要考查线段定比分点的有关计算.如下图可知.B点是有向线段PA的外分点..故选A.(5)某交高三年级有男生500人.女生400人.为了解该年级学生的健康情况.从男生中任意抽取25人.从女生中任意抽取20人进行调查.这种抽样方法是(A)简单随机抽样法 (B)抽签法(C)随机数表法 (D)分层抽样法[答案]D[解析]本小题主要考查抽样方法.若总体由差异明显的几部分组成时.经常采用分层抽样的方法进行抽样.故选D.(6)函数y=10x2-1 (0<x≤1=的反函数是(A) (B)(x>) (C) (<x≤ (D) (<x≤[答案]D[解析]本小题主要考查反函数的求法.由得:.即.又因为时..从而有.即原函数值域为.所以原函数的反函数为.故选D.(7)函数f(x)=的最大值为(A) (B) (C) (D)1[答案]B[解析]本小题主要考查均值定理.(当且仅.即时取等号.故选B.(8)若双曲线的左焦点在抛物线y2=2px的准线上.则p的值为(A)2 (B)3 (C)4 (D)4 [答案]C[解析]本小题主要考查双曲线和抛物线的几何性质.双曲线的左焦点坐标为:.抛物线的准线方程为.所以.解得:.故选C.(9)从编号为1,2,-,10的10个大小相同的球中任取4个.则所取4个球的最大号码是6的概率为(A) (B) (C) (D)[答案]B[解析]本小题主要考查组合的基本知识及等可能事件的概率..故选B.(10)若(x+)n的展开式中前三项的系数成等差数.则展开式中x4项的系数为(A)6 (B)7 (C)8 (D)9 [答案]B[解析]本小题主要考查二项式定理的基础知识.因为的展开式中前三项的系数..成等差数列.所以.即.解得:或(舍)..令可得..所以的系数为.故选B.图.模块①-⑤均由4个棱长为1的小正方体构成.模块⑥由15个棱长为1的小正方体构成.现从模块①-⑤中选出三个放到模块⑥上.使得模块⑥成为一个棱长为3的大正方体.则下列选择方案中.能够完成任务的为(A)模块①.②.⑤ (B)模块①.③.⑤(C)模块②.④.⑥ (D)模块③.④.⑤[答案]A[解析]本小题主要考查空间想象能力.先补齐中间一层.只能用模块⑤或①.且如果补①则后续两块无法补齐.所以只能先用⑤补中间一层.然后再补齐其它两块.(12)函数f(x)=的值域是(A)[-] (B)[-](C)[-] (D)[-][答案]C[解析]本小题主要考查函数值域的求法.令.则.当时..当且仅当时取等号.同理可得当时..综上可知的值域为.故选C.(13)已知集合.则 .[答案][解析]本小题主要考查集合的简单运算..(14)若则= .[答案]-23[解析]本小题主要考查指数的运算.上任意一点关于直线l:x-y+2=0 的对称点都在圆C上.则a= .[答案]-2[解析]本小题主要考查圆的一般方程及几何性质.由已知.直线经过了圆心.所以.从而有.(16)某人有3种颜色的灯泡.要在如题(16)图所示的6个点A.B.C.A1.B1.C1上各安装一个灯泡.要求同一条线段两端的灯泡不同色.则不同的安装方法共有 种.[答案]12[解析]本小题主要考查排列组合的基本知识.先安排底面三个顶点.共有种不同的安排方法.再安排上底面的三个顶点.共有种不同的安排方法.由分步记数原理可知.共有种不同的安排方法. 解:(Ⅰ)由余弦定理. (Ⅱ) 解:视“选择每道题的答案 为一次试验.则这是4次独立重复试验.且每次试验中“选择正确 这一事件发生的概率为. 由独立重复试验的概率计算公式得: (Ⅰ)恰有两道题答对的概率为 (Ⅱ)解法一:至少有一道题答对的概率为 解法二:至少有一道题答对的概率为 解:(Ⅰ)因 所以 即当 因斜率最小的切线与平行.即该切线的斜率为-12. 所以 解得 知 解:图.过点B′C∥A′A且使B′C=A′A.过点B作BD⊥CB′.交CB′的延长线于D.由已知AA′⊥l.可得DB′⊥l.又已知BB′⊥l.故l⊥平面BB′D.得BD⊥l又因BD⊥CB′.从而BD⊥平面α,BD之长即为点B到平面α的距离.因B′C⊥l且BB′⊥l.故∠BB′C为二面角α-l-β的平面角.由题意.∠BB′C=.因此在Rt△BB′D中.BB′=2,∠BB′D=π-∠BB′C=,BD=BB′?sinBB′D=.(Ⅱ)连接AC.BC.因B′C∥A′A.B′C=A′A,AA′⊥l,知A′ACB′为矩形.故AC∥l.所以∠BAC或其补角为异面直线l与AB所成的角.在△BB′C中.B′B=2.B′C=3.∠BB′C=.则由余弦定理.BC=.因BD平面.且DCCA.由三策划线定理知ACBC.故在△ABC中.∠BCA=.sinBAC=.因此.异面直线l与AB所成的角为arcsin解:(I)由双曲线的定义.点P的轨迹是以M.N为焦点.实轴长2a=2的双曲线.因此半焦距c=2.实半轴a=1.从而虚半轴b=,
网址:http://m.1010jiajiao.com/timu_id_75514[举报]
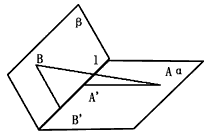
如图,α和β为平面,α∩β=l,A∈α,B∈β,AB=5,A,B在棱l上的射影分别为![]() .若二面角α―l―β的大小为
.若二面角α―l―β的大小为![]() ,求:
,求:
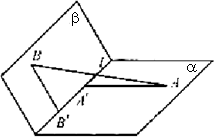
(Ⅰ)点B到平面α的距离;
(Ⅱ)异面直线l与AB所成的角(用反三角函数表示).
 如图,α和β为平面,α∩β=l,A∈α,B∈β,AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角α-l-β的大小为
如图,α和β为平面,α∩β=l,A∈α,B∈β,AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角α-l-β的大小为| 2π | 3 |
(Ⅰ)点B到平面α的距离;
(Ⅱ)异面直线l与AB所成的角(用反三角函数表示). 查看习题详情和答案>>
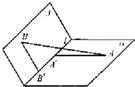
如图,α和β为平面,α∩β=l,A∈α,B∈β,AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2。若二面角α-l-β的大小为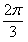 ,
,
求:(Ⅰ)点B到平面α的距离;
(Ⅱ)异面直线l与AB所成的角(用反三角函数表示)。
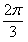 ,
,求:(Ⅰ)点B到平面α的距离;
(Ⅱ)异面直线l与AB所成的角(用反三角函数表示)。
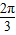 ,求:
,求: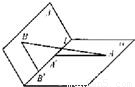
 ,求:
,求: