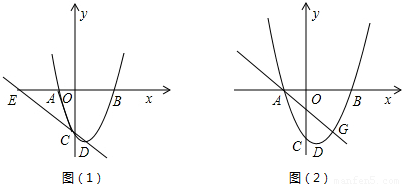摘要:(1)若∠A=600 求∠O. (2)如∠A=1000.l200.∠O又是多少? 你发现了什么规律? 当∠A的度数发生变化后.你的结论仍成立吗?(提示:三角形的内角和等于l800)
网址:http://m.1010jiajiao.com/timu_id_749687[举报]
已知,AB=BC,BD=BE,∠ABC=∠DBE=α,M、N分别是AD、CE的中点.

(1)如图1,若α=60゜,求∠BMN;
(2)如图2,若α=90゜,∠BMN=
(3)将图2的△BDE绕B点逆时针旋转一锐角,在图3中完成作图,则∠BMN=
查看习题详情和答案>>

(1)如图1,若α=60゜,求∠BMN;
(2)如图2,若α=90゜,∠BMN=
45°
45°
;(3)将图2的△BDE绕B点逆时针旋转一锐角,在图3中完成作图,则∠BMN=
45°
45°
.如图(1)所示,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D点,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),与y轴交于点C,且OB=OC,又tan∠ACO=
.
①求这个函数的表达式.
②经过C.D两点的直线与x轴交于点E,在抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,求点F的坐标.
③如图(2)所示,若G(2,t)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求此时P点的坐标和△APG的最大面积.

查看习题详情和答案>>
| 1 | 3 |
①求这个函数的表达式.
②经过C.D两点的直线与x轴交于点E,在抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,求点F的坐标.
③如图(2)所示,若G(2,t)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求此时P点的坐标和△APG的最大面积.


 .
.