��Ŀ����
��ͼ��1����ʾ����ƽ��ֱ������ϵ�У����κ���y=ax2+bx+c��a��0����ͼ��Ķ���ΪD�㣬��x�ύ��A��B���㣬��A��ԭ�����࣬��B������Ϊ��3��0������y�ύ�ڵ�C����OB=OC����tan��ACO=
��
������������ı���ʽ��
�ھ���C��D�����ֱ����x�ύ�ڵ�E�������������Ƿ���������ĵ�F��ʹ�Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ����F�����꣮
����ͼ��2����ʾ����G��2��t���Ǹ���������һ�㣬��P��ֱ��AG�·�����������һ���㣬����P�˶���ʲôλ��ʱ����APG�����������ʱP�������͡�APG����������
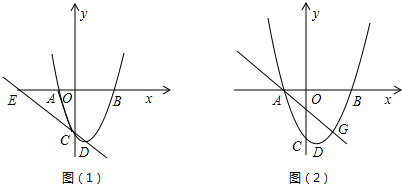
| 1 | 3 |
������������ı���ʽ��
�ھ���C��D�����ֱ����x�ύ�ڵ�E�������������Ƿ���������ĵ�F��ʹ�Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ����F�����꣮
����ͼ��2����ʾ����G��2��t���Ǹ���������һ�㣬��P��ֱ��AG�·�����������һ���㣬����P�˶���ʲôλ��ʱ����APG�����������ʱP�������͡�APG����������
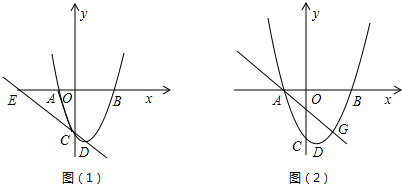
��������1��������֪�����������C��A�����꣬���ô���ϵ������������ߵĽ���ʽ��
��2�������Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ���ƽ���ı��ε������Լ����κ��������ʵó�AE=CF��AE��CF���ɵó��𰸣�
��3�������AC�ij�������AC��Ϊ��ֵ����P��ֱ��AG�ľ������ʱ����APG�������ɹ�P��y���ƽ���ߣ���AG��Q�����P�����꣬����ֱ��AG�Ľ���ʽ�����Q�����꣬Ҳ�����PQ�ij��������ɵó����ڡ�APG�������P������ĺ�����ϵʽ�����ݺ��������ʿ������APG����������P������꣬���ݴ�ʱ��APG�������AG�ij����������P��ֱ��AC�������룮
��2�������Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ���ƽ���ı��ε������Լ����κ��������ʵó�AE=CF��AE��CF���ɵó��𰸣�
��3�������AC�ij�������AC��Ϊ��ֵ����P��ֱ��AG�ľ������ʱ����APG�������ɹ�P��y���ƽ���ߣ���AG��Q�����P�����꣬����ֱ��AG�Ľ���ʽ�����Q�����꣬Ҳ�����PQ�ij��������ɵó����ڡ�APG�������P������ĺ�����ϵʽ�����ݺ��������ʿ������APG����������P������꣬���ݴ�ʱ��APG�������AG�ij����������P��ֱ��AC�������룮
����⣺��1������һ���ߵ�B������Ϊ��3��0������y�ύ�ڵ�C����OB=OC����tan��ACO=
��
��tan��ACO=
=
��
��AO=1��
��C��0��-3����A��-1��0����
��A��B��C�������������
��
��ã�
��
����������κ����ı���ʽΪ��y=x2-2x-3
������������֪�ã�C��0��-3����A��-1��0����
��ñ���ʽΪ��y=a��x+1����x-3����
��C����������ã�a=1��
����������κ����ı���ʽΪ��y=x2-2x-3��
��ע������ʽ�����ս����������ʽ�е���һ�ֶ����۷֣�
��2����ͼ����y=x2-2x-3�У���x=0����y=-3��
��y=0����x2-2x-3=0����x1=-1��x2=3��
��A��-1��0����B��3��0����C��0��-3����
��y=��x-1��2-4���ඥ��D��1��-4����
�������ֱ��CD�ı���ʽ��y=-x-3��
��y=-x-3����y=0����x=-3��
��E��-3��0����
��AE=2��
��y=x2-2x-3����y=-3����x1=0��x2=2��
��CF=2��
��AE=CF��
��AE��CF��
���ı���AECFΪƽ���ı��Σ���ʱF��2��-3����
 ��3������P��y���ƽ������AG���ڵ�Q��
��3������P��y���ƽ������AG���ڵ�Q��
��G��2��-3����ֱ��AGΪy=-x-1��
��P��x��x2-2x-3������Q��x��-x-1����PQ=-x2+x+2��
S��APG=S��APQ+S��GPQ=
(-x2+x+2)��3=-
(x-
)2+
��
��x=
ʱ����APG��������Ϊ
��
��AG=3
��P��AG��������Ϊ
=
=
��
��ʱP�������Ϊ(
��-
)��
| 1 |
| 3 |
��tan��ACO=
| AO |
| CO |
| 1 |
| 3 |
��AO=1��
��C��0��-3����A��-1��0����
��A��B��C�������������
|
��ã�
|
����������κ����ı���ʽΪ��y=x2-2x-3
������������֪�ã�C��0��-3����A��-1��0����
��ñ���ʽΪ��y=a��x+1����x-3����

��C����������ã�a=1��
����������κ����ı���ʽΪ��y=x2-2x-3��
��ע������ʽ�����ս����������ʽ�е���һ�ֶ����۷֣�
��2����ͼ����y=x2-2x-3�У���x=0����y=-3��
��y=0����x2-2x-3=0����x1=-1��x2=3��
��A��-1��0����B��3��0����C��0��-3����
��y=��x-1��2-4���ඥ��D��1��-4����
�������ֱ��CD�ı���ʽ��y=-x-3��
��y=-x-3����y=0����x=-3��
��E��-3��0����
��AE=2��
��y=x2-2x-3����y=-3����x1=0��x2=2��
��CF=2��
��AE=CF��
��AE��CF��
���ı���AECFΪƽ���ı��Σ���ʱF��2��-3����
 ��3������P��y���ƽ������AG���ڵ�Q��
��3������P��y���ƽ������AG���ڵ�Q����G��2��-3����ֱ��AGΪy=-x-1��
��P��x��x2-2x-3������Q��x��-x-1����PQ=-x2+x+2��
S��APG=S��APQ+S��GPQ=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 27 |
| 8 |
��x=
| 1 |
| 2 |
| 27 |
| 8 |
��AG=3
| 2 |
| 2S��APG |
| AG |
2��
| ||
3
|
| 9 |
| 8 |
| 2 |
��ʱP�������Ϊ(
| 1 |
| 2 |
| 15 |
| 4 |
���������⿼���˶��κ�������ʽ��ȷ����ƽ���ı��ε��ж���ͼ���������֪ʶ���ۺ���ǿ������Ҫ��ϸߣ�����ѧ�����ν�ϵ���ѧ˼�뷽����

��ϰ��ϵ�д�
 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�
�����Ŀ


 .��ش��������⣺
.��ش��������⣺