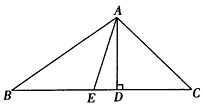
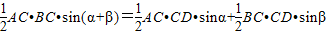摘要：2．比较:与1.5的大小如下图.在△ABC中.AC=BC.∠ACB=90°.BD平分∠ABC.且AE垂直BD的延长线于E.
网址：http://m.1010jiajiao.com/timu_id_749646[举报]
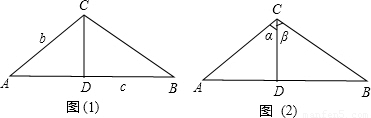
如图（1），由直角三角形边角关系，可将三角形面积公式变形得到S△ABC=
bcsinA…①
即三角形的面积等于两边之长与夹角正弦值之积的一半
如图，在△ABC中，CD⊥AB于D，∠ACD=α，∠DCB=β
∵S△ABC=S△ACD+S△BCD，由公式①得到
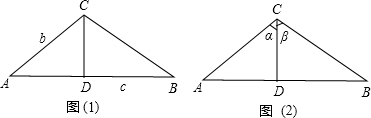
AC•BC•sin(α+β)=
AC•CD•sinα+
BC•CD•sinβ
即AC•BC•sin（α+β）=AC•CD•sinα+BC•CD•sinβ…②
你能利用直角三角形关系及等式基本性质，消去②中的AC、BC、CD吗？若不能，说明理由；若能，写出解决过程．并利用结论求出sin75°的值．
查看习题详情和答案>>
| 1 |
| 2 |
即三角形的面积等于两边之长与夹角正弦值之积的一半
如图，在△ABC中，CD⊥AB于D，∠ACD=α，∠DCB=β
∵S△ABC=S△ACD+S△BCD，由公式①得到
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即AC•BC•sin（α+β）=AC•CD•sinα+BC•CD•sinβ…②
你能利用直角三角形关系及等式基本性质，消去②中的AC、BC、CD吗？若不能，说明理由；若能，写出解决过程．并利用结论求出sin75°的值．
查看习题详情和答案>>
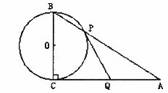
如下图，在△ABC中，∠BCA=90°，以BC为直径的⊙O交AB于点P，Q是AC的中点。
（1）判断PQ与⊙O的位置关系，并说明理由。
（2）若⊙O 的半径是1.5，PQ=2，求AB的长。
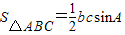…①
