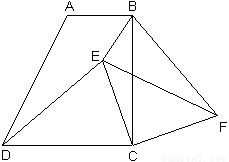
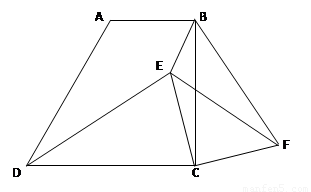摘要：21．如下图.在梯形ABCD中.AB∥DC.E是BC的中点.AE.DC的延长线相交于点F.连结AC.BF．
网址：http://m.1010jiajiao.com/timu_id_748536[举报]
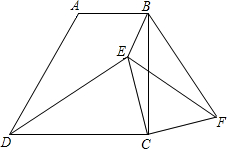如图，在梯形ABCD中，AB∥DC，∠ABC=90°，AB=2，BC=4，tan∠ADC=2．（1）求证：DC=BC；
（2）E是梯形内一点，连接DE、CE，将△DCE绕点C顺时针旋转90°，得△BCF，连接EF．判断EF与CE的数量关系，并证明你的结论；
（3）在（2）的条件下，当CE=2BE，∠BEC=135°时，求cos∠BFE的值． 查看习题详情和答案>>
如图，在梯形ABCD中， AB∥DC，∠BCD＝90°，且AB＝1，BC＝2，
tan∠ADC＝2．
⑴求证：DC＝BC；
⑵E是梯形内的一点，F是梯形外的一点，且∠EDC＝∠FBC，DE＝BF，试判断△ECF的形状，并证明你的结论；⑶在⑵的条件下，当BE：CE＝1：2，∠BEC＝135°时，求sin∠BFE的值．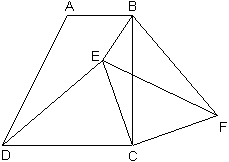
如图，在梯形ABCD中，AB∥DC，∠ABC＝90°，AB＝2，BC＝4，tan∠ADC＝2.
（1）求证：DC＝BC；
（2）E是梯形内一点，连接DE、CE，将△DCE绕点C顺时针旋转90°，得△BCF，连接EF.判断EF与CE的数量关系，并证明你的结论；
（3）在（2）的条件下，当CE＝2BE，∠BEC＝135°时，求cos∠BFE的值.
