摘要:(1)操作1:固定△ABC.将三角板沿C→B方向平移.使其直角顶点落在BC的中点M.如图2示.探究:三角板沿C→B方向平移的距离为 情形下.将三角板绕BC的中点M顺时针方向旋转角度α 如图3示.探究:设三角板两直角边分别与AB.AC交于P.Q.观察四边形MPAQ形状的变化.发现其面积始终不变.那么四边形MPAQ的面积S四边形MPAQ= 的情形下.连PQ.设BP=x,记△APQ的面积为y, 试求y关于x的函数关系式,并求x为何值时.△PQA面积有最大值.最大值是多少?
网址:http://m.1010jiajiao.com/timu_id_744674[举报]
两只全等的直角三角板ABC和DEF重叠在一起,其中∠A=60°,AC=4.固定△ABC不动,将△DEF进行如下操作:
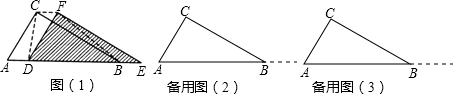
(1)如图 (1),将△DEF沿线段AB以1cm/s的速度向右平移(即D点在线段AB内移动),连接DC、CF、FB,显然,随着时间x的变化,四边形CDBF的形状在不断的变化,探究它的面积是否变化:如果变化,试用x的代数式表示四边形CDBF的面积S;如果不变,说明理由,并求出其面积.
(2)在备用图(2)中尝试解决:
①运动过程中四边形CDBF有可能是正方形吗?如果可能,求出x,如果没有简要说明理由.
②当x为何值时,四边形CDBF为菱形?说明理由.
(3)如图(3),在(2)②的情况下,将△DEF的D点固定,然后绕D点按顺时针方向旋转△DEF,连接AE,设∠AED=α,旋转的角度为β,
①当β=60°时,画出图形,并请你求出sinα的值.
②当0°≤β≤180°时,试写出sinα的最大值.
查看习题详情和答案>>

(1)如图 (1),将△DEF沿线段AB以1cm/s的速度向右平移(即D点在线段AB内移动),连接DC、CF、FB,显然,随着时间x的变化,四边形CDBF的形状在不断的变化,探究它的面积是否变化:如果变化,试用x的代数式表示四边形CDBF的面积S;如果不变,说明理由,并求出其面积.
(2)在备用图(2)中尝试解决:
①运动过程中四边形CDBF有可能是正方形吗?如果可能,求出x,如果没有简要说明理由.
②当x为何值时,四边形CDBF为菱形?说明理由.
(3)如图(3),在(2)②的情况下,将△DEF的D点固定,然后绕D点按顺时针方向旋转△DEF,连接AE,设∠AED=α,旋转的角度为β,
①当β=60°时,画出图形,并请你求出sinα的值.
②当0°≤β≤180°时,试写出sinα的最大值.
两只全等的直角三角板ABC和DEF重叠在一起,其中∠A=60°,AC=4.固定△ABC不动,将△DEF进行如下操作:
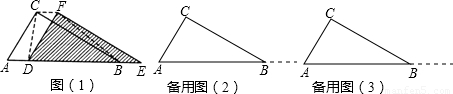
(1)如图 (1),将△DEF沿线段AB以1cm/s的速度向右平移(即D点在线段AB内移动),连接DC、CF、FB,显然,随着时间x的变化,四边形CDBF的形状在不断的变化,探究它的面积是否变化:如果变化,试用x的代数式表示四边形CDBF的面积S;如果不变,说明理由,并求出其面积.
(2)在备用图(2)中尝试解决:
①运动过程中四边形CDBF有可能是正方形吗?如果可能,求出x,如果没有简要说明理由.
②当x为何值时,四边形CDBF为菱形?说明理由.
(3)如图(3),在(2)②的情况下,将△DEF的D点固定,然后绕D点按顺时针方向旋转△DEF,连接AE,设∠AED=α,旋转的角度为β,
①当β=60°时,画出图形,并请你求出sinα的值.
②当0°≤β≤180°时,试写出sinα的最大值.
查看习题详情和答案>>

(1)如图 (1),将△DEF沿线段AB以1cm/s的速度向右平移(即D点在线段AB内移动),连接DC、CF、FB,显然,随着时间x的变化,四边形CDBF的形状在不断的变化,探究它的面积是否变化:如果变化,试用x的代数式表示四边形CDBF的面积S;如果不变,说明理由,并求出其面积.
(2)在备用图(2)中尝试解决:
①运动过程中四边形CDBF有可能是正方形吗?如果可能,求出x,如果没有简要说明理由.
②当x为何值时,四边形CDBF为菱形?说明理由.
(3)如图(3),在(2)②的情况下,将△DEF的D点固定,然后绕D点按顺时针方向旋转△DEF,连接AE,设∠AED=α,旋转的角度为β,
①当β=60°时,画出图形,并请你求出sinα的值.
②当0°≤β≤180°时,试写出sinα的最大值.
查看习题详情和答案>>
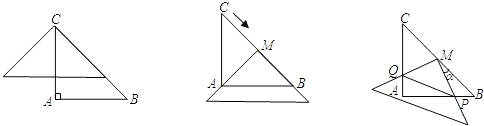
如图,在△ABC中,AC=AB=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠.
(1)操作1:固定△ABC,将三角板沿C→B方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿C→B方向平移的距离为 ;
(2)操作2:在(1)的情况下,将三角板BC的中点M顺时针方向旋转角度a(0°<a<90°),如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
(3)在(2)的情形下,连PQ,设BP=x,记△MPQ的面积为y,试求y关于x的函数关系式,并求x为何值时,y的值是四边形MPAQ的面积的一半,此时,指出四边形MPAQ的形状.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)操作1:固定△ABC,将三角板沿C→B方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿C→B方向平移的距离为
(2)操作2:在(1)的情况下,将三角板BC的中点M顺时针方向旋转角度a(0°<a<90°),如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
(3)在(2)的情形下,连PQ,设BP=x,记△MPQ的面积为y,试求y关于x的函数关系式,并求x为何值时,y的值是四边形MPAQ的面积的一半,此时,指出四边形MPAQ的形状.
 查看习题详情和答案>>
查看习题详情和答案>>
如图,在△ABC中,AC=AB=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠.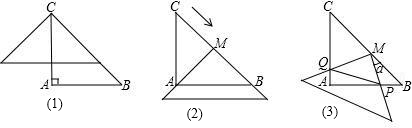
(1)操作1:固定△ABC,将三角板沿C?B方向平移,使其直角顶点落在BC的中点M,如图2示.探究:三角板沿C?B方向平移的距离为 ;
(2)操作2:在(1)情形下,将三角板绕BC的中点M顺时针方向旋转角度α(0°<α<90°)如图3示.探究:设三角板两直角边分别与AB、AC交于P、Q,观察四边形MPAQ形状的变化,发现其面积始终不变,那么四边形MPAQ的面积S四边形MPAQ= ;
(3)在(2)的情形下,连PQ,设BP=x,记△APQ的面积为y,试求y关于x的函数关系式;并求x为何值时,△PQA面积有最大值,最大值是多少? 查看习题详情和答案>>

(1)操作1:固定△ABC,将三角板沿C?B方向平移,使其直角顶点落在BC的中点M,如图2示.探究:三角板沿C?B方向平移的距离为
(2)操作2:在(1)情形下,将三角板绕BC的中点M顺时针方向旋转角度α(0°<α<90°)如图3示.探究:设三角板两直角边分别与AB、AC交于P、Q,观察四边形MPAQ形状的变化,发现其面积始终不变,那么四边形MPAQ的面积S四边形MPAQ=
(3)在(2)的情形下,连PQ,设BP=x,记△APQ的面积为y,试求y关于x的函数关系式;并求x为何值时,△PQA面积有最大值,最大值是多少? 查看习题详情和答案>>
