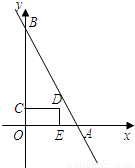摘要：解答下列问题:.点C的坐标为(2.1).写出此时点B的坐标,(2)请你在图②中画出第二个叶片F2,的条件下.连接OB.由第一个叶片逆时针旋转180°得到第二个叶片的过程中.线段OB扫过的图形面积是多少?
网址：http://m.1010jiajiao.com/timu_id_744670[举报]
（1）阅读理解：配方法是中学数学的重要方法，用配方法可求最大（小）值．
对于任意正实数a、b，可作如下变形a+b=(
)2+(
)2=(
)2+(
)2-2
+2
=(
-
)2+2
，
又∵(
-
)2≥0，∴(
-
)2+2
≥0+2
，即a+b≥2
．
根据上述内容，回答下列问题：在a+b≥2
（a、b均为正实数）中，若ab为定值p，则a+b≥2
，当且仅当a、b满足 时，a+b有最小值2
．
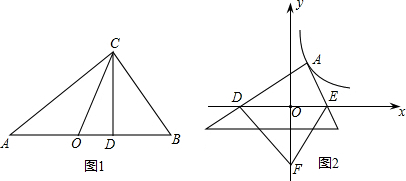
（2）思考验证：如图1，△ABC中，∠ACB=90°，CD⊥AB，垂足为D，CO为AB边上中线，AD=2a，DB=2b，试根据图形验证a+b≥2
成立，并指出等号成立时的条件．
（3）探索应用：如图2，已知A为反比例函数y=
的图象上一点，A点的横坐标为1，将一块三角板的直角顶点放在A处旋转，保持两直角边始终与x轴交于两点D、E，F（0，-3）为y轴上一点，连接DF、EF，求四边形ADFE面积的最小值．
查看习题详情和答案>>
对于任意正实数a、b，可作如下变形a+b=(
| a |
| b |
| a |
| b |
| ab |
| ab |
| a |
| b |
| ab |
又∵(
| a |
| b |
| a |
| b |
| ab |
| ab |
| ab |
根据上述内容，回答下列问题：在a+b≥2
| ab |
| p |
| p |
（2）思考验证：如图1，△ABC中，∠ACB=90°，CD⊥AB，垂足为D，CO为AB边上中线，AD=2a，DB=2b，试根据图形验证a+b≥2
| ab |
（3）探索应用：如图2，已知A为反比例函数y=
| 4 |
| x |
查看习题详情和答案>>
如图，点A、B的坐标分别为（4，0）、（0，8），点C是线段OB上一动点，点E在x轴正半轴上，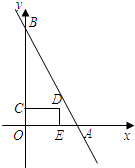
四边形OEDC是矩形，且OE=2OC．设OE=t（t＞0），矩形OEDC与△AOB重合部分的面积为S．
根据上述条件，回答下列问题：
（1）当矩形OEDC的顶点D在直线AB上时，求t的值；
（2）当t=4时，求S的值；
（3）直接写出S与t的函数关系式（不必写出解题过程）；
（4）若S=12，则t= ．
查看习题详情和答案>>
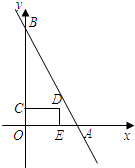四边形OEDC是矩形，且OE=2OC．设OE=t（t＞0），矩形OEDC与△AOB重合部分的面积为S．根据上述条件，回答下列问题：
（1）当矩形OEDC的顶点D在直线AB上时，求t的值；
（2）当t=4时，求S的值；
（3）直接写出S与t的函数关系式（不必写出解题过程）；
（4）若S=12，则t=
四边形OEDC是矩形，且OE=2OC．设OE=t（t＞0），矩形OEDC与△AOB重合部分的面积为S．
坐标分别为（4，0）、（0，8），点
是线段
上一动点，点
在
轴正半轴上，四边形
是矩形，且
．设
，矩形
重合部分的面积为
．根据上述条件，回答下列问题：
在直线
上时，求
的值；
时，求
，则
．
