摘要:C.若.则 D.有两边相等的三角形是等腰三角形
网址:http://m.1010jiajiao.com/timu_id_741658[举报]
(创新题)“有两边相等的两个直角三角形全等”这个命题对与否,甲、乙、丙三位同学给出了如下论断:
甲:正确.因为若两边都是直角边,则用(S.A.S.)全等识别法就可以证它们全等.
乙:正确.因为若其中一边是直角边,另一边是斜边,则可用(H. L.)定理证全等.
丙:不正确.若一个三角形较长的直角边与另一三角形斜边相等,较短的直角边与另一三角形较长的直角边相等,则显而易见两个三角形不全等.
请你就这三个同学的见解发表自己的意见.
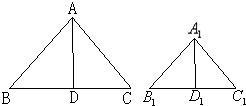
1、两个三角形相似,除了对应边成比例、对应角相等之外,还可以得到许多有用的结果.如图,△ABC∽△A1B1C1,相似比为k.
(1)若AD、A1D1分别为BC、B1C1边上的高,则AD与A1D1之比为
(2)若AD、A1D1分别为对应边BC、B1C1上的中线,则AD与A1D1之比为
(3)若AD、A1D1分别为对应角的角平分线,则AD与A1D1之比为
(4)△ABC与△A1B1C1的周长比为
(5)△ABC与△A1B1C1的面积比为
查看习题详情和答案>>
(1)若AD、A1D1分别为BC、B1C1边上的高,则AD与A1D1之比为
k
,也就是说:相似三角形对应高的比等于相似比
;(2)若AD、A1D1分别为对应边BC、B1C1上的中线,则AD与A1D1之比为
k
,也就是说:相似三角形对应中线的比等于相似比
;(3)若AD、A1D1分别为对应角的角平分线,则AD与A1D1之比为
k
,也就是说:相似三角形对应角平分线的比等于相似比
;(4)△ABC与△A1B1C1的周长比为
k
;(5)△ABC与△A1B1C1的面积比为
k2
.