摘要:24.已知:如图.∥.
网址:http://m.1010jiajiao.com/timu_id_739478[举报]
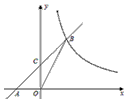
已知:如图,函数y=-x+2的图象与x轴、y轴分别交于点A、B,一直线 经过点C(1,0),将△AOB的面积分成相等的两部分。
经过点C(1,0),将△AOB的面积分成相等的两部分。
 经过点C(1,0),将△AOB的面积分成相等的两部分。
经过点C(1,0),将△AOB的面积分成相等的两部分。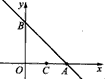
(1)求直线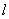 的函数解析式;
的函数解析式;
(2)若直线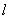 将△AOB的面积分成1:3两部分,求直线
将△AOB的面积分成1:3两部分,求直线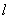 的函数解析式。
的函数解析式。
查看习题详情和答案>>
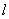 的函数解析式;
的函数解析式; (2)若直线
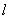 将△AOB的面积分成1:3两部分,求直线
将△AOB的面积分成1:3两部分,求直线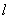 的函数解析式。
的函数解析式。 已知:如图,直线l: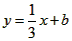 经过点
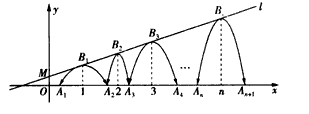
经过点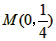 ,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1)。
,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1)。
(1)求b的值;
(2)求经过点A1、B1、A2的抛物线的解析式(用含d的代数式表示);
(3)定义:若抛物线的顶点与x轴的两个交点构成的三角形,则这种抛物线就称为“美丽抛物线”。
探究:当d(0<d<1)的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,清你求出相应的d 的值。
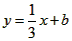 经过点
经过点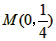 ,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1)。
,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1)。(1)求b的值;
(2)求经过点A1、B1、A2的抛物线的解析式(用含d的代数式表示);
(3)定义:若抛物线的顶点与x轴的两个交点构成的三角形,则这种抛物线就称为“美丽抛物线”。
探究:当d(0<d<1)的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,清你求出相应的d 的值。
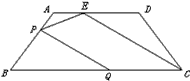
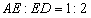 ,连结CE。点P是AB边上的一个动点,过点P作PQ⊥CE,交BC于点Q。设
,连结CE。点P是AB边上的一个动点,过点P作PQ⊥CE,交BC于点Q。设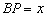 ,
,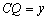 ,
,
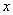 的值。
的值。 的图象上,点D的坐标为(0,-2)。
的图象上,点D的坐标为(0,-2)。