摘要：D.各组组中值分别为64.5.75.5.84.5.94.5
网址：http://m.1010jiajiao.com/timu_id_737723[举报]
一次测试八年级若干名学生1分钟跳绳次数的频数分布直方图如图所示，请根据这个直方图回答下列问题：（1）已知自左至右第2、3组（组中值分别为145、155）的频率之和为0.28，第3、4、5组（组中值分别为155、165、175）的频率之和为0.8，则参加测试的总人数有
50
50
人，第3组的频数为8
8
人，第4组的频率为0.4
0.4
，并将直方图补充完整；（2）若图中自左至右各组的跳绳平均次数分别为137次，146次，156次，164次，177次，则参加测试的学生跳绳的平均次数为
| 137×4+146×6+156×8+164×20+177×12 |
| 50 |
| 137×4+146×6+156×8+164×20+177×12 |
| 50 |
（3）若测试所得数据的中位数是160次，则测试次数为160次的学生至少有
8
8
人．（直方图中每一组包括前一个边界值，不包括后一个边界值）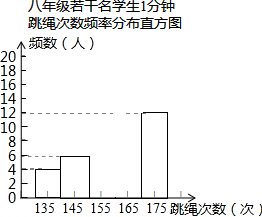
一次测试八年级若干名学生1分钟跳绳次数的频数分布直方图如图所示，请根据这个直方图回答下列问题：
（1）已知自左至右第2、3组（组中值分别为145、155）的频率之和为0.28，第3、4、5组（组中值分别为155、165、175）的频率之和为0.8，则参加测试的总人数有______人，第3组的频数为______人，第4组的频率为______，并将直方图补充完整；
（2）若图中自左至右各组的跳绳平均次数分别为137次，146次，156次，164次，177次，则参加测试的学生跳绳的平均次数为______（只需列出算式，不用计算结果）；
（3）若测试所得数据的中位数是160次，则测试次数为160次的学生至少有______人．（直方图中每一组包括前一个边界值，不包括后一个边界值）
查看习题详情和答案>>
如图，△ABC中，各顶点的坐标分别为A（-1，3），B（-3，2），C（-2，1）．已知△DEF与△ABC关于原点对称，且A，B的对称点分别为D，E．（1）写出△DEF各顶点的坐标，并在坐标系中画出△DEF；
（2）若点A的横坐标增加m，则点D的坐标是多少？
（3）若△ABC绕原点旋转后，△DEF也随着旋转，这时点F的坐标变为（3a-1，
| 1 |
| 2 |
| 3 |
| 2 |
阅读材料：
如图，△ABC中，AB=AC，P为底边BC上任意一点，点P到两腰的距离分别为r1，r2，腰上的高为h，连接AP，则S△ABP+S△ACP=S△ABC，即：
AB•r1+
AC•r2=
AB•h，∴r1+r2=h（定值）．
（1）类比与推理
如果把“等腰三角形”改成“等边三角形”，那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”，即：已知等边△ABC内任意一点P到各边的距离分别为r1，r2，r3，等边△ABC的高为h，试证明r1+r2+r3=h（定值）．
（2）理解与应用
△ABC中，∠C=90°，AB=10，AC=8，BC=6，△ABC内部是否存在一点O，点O到各边的距离相等？ （填“存在”或“不存在”），若存在，请直接写出这个距离r的值，r= ．若不存在，请说明理由．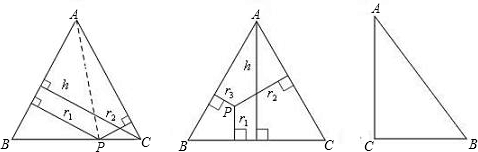
查看习题详情和答案>>
如图，△ABC中，AB=AC，P为底边BC上任意一点，点P到两腰的距离分别为r1，r2，腰上的高为h，连接AP，则S△ABP+S△ACP=S△ABC，即：
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
（1）类比与推理
如果把“等腰三角形”改成“等边三角形”，那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”，即：已知等边△ABC内任意一点P到各边的距离分别为r1，r2，r3，等边△ABC的高为h，试证明r1+r2+r3=h（定值）．
（2）理解与应用
△ABC中，∠C=90°，AB=10，AC=8，BC=6，△ABC内部是否存在一点O，点O到各边的距离相等？
查看习题详情和答案>>
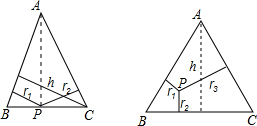
（2013•德城区二模）阅读材料：如图，△ABC中，AB=AC，P为底边BC上任意一点，点P到两腰的距离分别为r1，r2，腰上的高为h，连接AP，则S△ABP+S△ACP=S△ABC，即：
AB•r1+
AC•r2=
AB•h，∴r1+r2=h
（1）理解与应用
如果把“等腰三角形”改成“等边三角形”，那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”，即：已知边长为2的等边△ABC内任意一点P到各边的距离分别为r1，r2，r3，试证明：r1+r2+r3=
．
（2）类比与推理
边长为2的正方形内任意一点到各边的距离的和等于
（3）拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为r1，r2，…rn，请问r1+r2+…rn是否为定值（用含n的式子表示），如果是，请合理猜测出这个定值．
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
（1）理解与应用
如果把“等腰三角形”改成“等边三角形”，那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”，即：已知边长为2的等边△ABC内任意一点P到各边的距离分别为r1，r2，r3，试证明：r1+r2+r3=
| 3 |
（2）类比与推理
边长为2的正方形内任意一点到各边的距离的和等于
4
4
；（3）拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为r1，r2，…rn，请问r1+r2+…rn是否为定值（用含n的式子表示），如果是，请合理猜测出这个定值．