摘要：24．[尝试]如图(一).把一个等腰Rt△ABC沿斜边上的中线CD剪一刀.把分割成的两部分拼成一个四边形A'BCD.如图所示.(以下有画图要求的.所用工具不限.不必写画法和证明) (1)猜一猜:四边形A'BCD一定是 , (2)试一试:按上述的剪裁方法.请你拼一个与图(一)不同的四边形.并在图(二)中画出图形．
网址：http://m.1010jiajiao.com/timu_id_737362[举报]
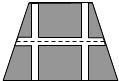如图，要设计一个等腰梯形的花坛，花坛上底长100m，下底长180m，上下底相距80m，在两腰中点连线外有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等，甬道的面积是梯形面积的六分之一．甬道的宽应是多少（精确到0.01m）？（友情提示：中间甬道的中位线就是等腰梯形的中位线） 查看习题详情和答案>>
如图，要设计一个等腰梯形的花坛，花坛上底长12米，下底长18米，高8米．（1）求梯形的中位线的长；
（2）在梯形两腰中点连线（虚线）处有一条横向通道，上下底之间有两条纵向通道，各条通道的宽度均为x米．
①若通道的总面积等于42平方米，求通道的宽；
②按要求通道的宽不能超过1米，且修建三条通道应付的工资合计为25
| 3 |
| 3 |
如图，要设计一个等腰梯形的花坛，花坛上底长240m，下底长360m，上下底相距80m，在两腰中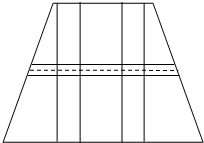
点连线（虚线）处有一条横向梯形通道，上下底之间有两条纵向矩形通道，横、纵通道的宽度分别为x（m）、2x（m）．
（1）当三条通道的面积是梯形面积的
时，求每条纵向通道的宽；
（2）根据设计的要求，横向通道的宽不能超过6m．如果修建通道的总费用为11.4x万元，花坛其余部分的绿化费用为每平方米0.02万元，那么当横向通道的宽度为多少m时，所建花坛的总费用最少？最少费用是多少万元？ 查看习题详情和答案>>
点连线（虚线）处有一条横向梯形通道，上下底之间有两条纵向矩形通道，横、纵通道的宽度分别为x（m）、2x（m）．（1）当三条通道的面积是梯形面积的
| 1 | 8 |
（2）根据设计的要求，横向通道的宽不能超过6m．如果修建通道的总费用为11.4x万元，花坛其余部分的绿化费用为每平方米0.02万元，那么当横向通道的宽度为多少m时，所建花坛的总费用最少？最少费用是多少万元？ 查看习题详情和答案>>
如图，要设计一个等腰梯形的花坛，花坛上底长120米，下底长180米，上下底相距80米，在两腰中点连线（虚线）处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．要使花坛栽花部分（图示阴影部分）的面积达到10000平方米，求甬道的宽度时，设甬道的宽为x米，可列方程得：310x-2x2=10000
310x-2x2=10000
．
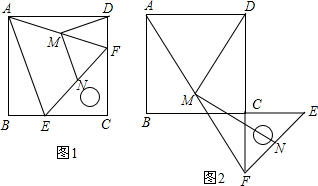（2013•山西模拟）操作与证明：如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF．取AF中点M，EF的中点N，连接MD、MN．（1）连接AE，求证：△AEF是等腰三角形；
猜想与发现：
（2）在（1）的条件下，请判断MD、MN的数量关系和位置关系，得出结论．
结论1：DM、MN的数量关系是
相等
相等
；结论2：DM、MN的位置关系是
垂直
垂直
；拓展与探究：
（3）如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．