题目内容
如图，要设计一个等腰梯形的花坛，花坛上底长120米，下底长180米，上下底相距80米，在两腰中点连线（虚线）处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．要使花坛栽花部分（图示阴影部分）的面积达到10000平方米，求甬道的宽度时，设甬道的宽为x米，可列方程得：310x-2x2=10000
310x-2x2=10000
．分析：根据题意得出甬道总面积为各甬道面积之和，即150x+160x-2x2=310x-2x2，根据面积为10000平方米即可求解．
解答：解：横向甬道的面积为：
x=150x（m2）；纵向甬道的面积为2×80x=160x（m2）；
甬道总面积为150x+160x-2x2=310x-2x2，
依题意得：310x-2x2=10000．
故答案为：310x-2x2=10000．
| 120+180 |
| 2 |
甬道总面积为150x+160x-2x2=310x-2x2，
依题意得：310x-2x2=10000．
故答案为：310x-2x2=10000．
点评：本题考查了一元二次方程的应用，解答本题的关键是正确表示出纵、横甬道的面积，难度一般．
练习册系列答案
中考解读考点精练系列答案
相关题目
25、如图，要设计一个等腰梯形的花坛，花坛上底长120米，下底长180米，上下底相距80米，在两腰中点连线（虚线）处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．设甬道的宽为x米．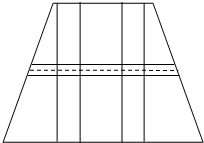
点连线（虚线）处有一条横向梯形通道，上下底之间有两条纵向矩形通道，横、纵通道的宽度分别为x（m）、2x（m）．
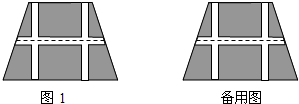（2012•广西模拟）如图，要设计一个等腰梯形的花坛，花坛上底120米，下底180米，上下底相距80米，在两腰中点连线（虚线）处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．设甬道的宽为x米．
（2011•锦江区模拟）如图，要设计一个等腰梯形的花坛，花坛上底长120米，下底长180米，上下底相距80米，在两腰中点连线（虚线）处有一条横向通道，上下底之间有两条纵向通道，各通道的宽度相等．设通道的宽为x米．