摘要：23．如下图所示.在等腰梯形ABCD中.AD∥BC.AB＝CD.点P为BC边上任意一点.且PE⊥AB.PF⊥CD.BG⊥CD.垂足分别为E.F.G.请你探索PE.PF 与BG的长度关系?并证明你的结论．
网址：http://m.1010jiajiao.com/timu_id_737360[举报]
如下图所示，在等腰梯形ABCD中，BC∥AD，BC＝8，AD＝20，AB＝DC＝10，点P从A点出发，沿AD边向点D移动，点Q自A点出发，沿A→B→C的路线移动，且PQ∥DC，若AP＝x，梯形位于线段PQ右侧部分的面积为S．
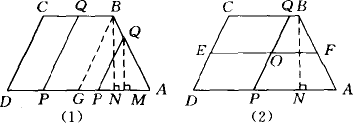
(1)分别求出当点Q位于AB，BC上时，S与x之间的函数关系式，并写出自变量x的取值范围；
(2)当线段PQ将梯形ABCD分成面积相等的两部分时，x的值是多少？
(3)在(2)的条件下，设线段PQ与梯形ABCD的中位线EF交于O点，那么OE与OF的长度有什么关系？请说明理由，并进一步研究：对任何一个梯形，当一直线L经过梯形中位线的中点并满足什么条件时，它一定平分梯形的面积？(只要求说出条件，不需要证明)
如图所示，在等腰梯形ABCD中，AD∥BC，AC与BD相交于O点，有如下四个结论：(1)AC＝BD；(2)梯形ABCD是中心对称图形；(3)∠ADB＝∠DAC；(4)△AOD∽△COB．
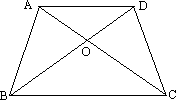
请把正确的结论的序号填在横线上________．
查看习题详情和答案>>
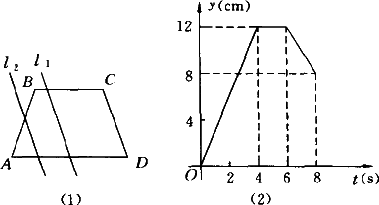
如图①，在等腰梯形ABCD中，AD∥BC，AB=CD，上底AD=2，梯形的高也等于2．一动点P从C出发，沿CB方向在线段BC上作匀速运动．