摘要：在梯形ABCD中.AB∥CD.∠A=90°. AB=2.BC=3.CD=1.E是AD中点． 求证:CE⊥BE．
网址：http://m.1010jiajiao.com/timu_id_737263[举报]
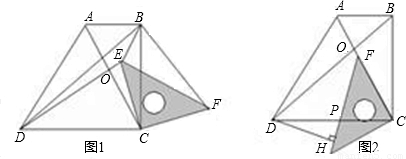
在梯形ABCD中，AB∥CD，∠BCD=90°，且AB=1，BC=2，tan∠ADC=2；对角线相交于O点，等腰直角三角板的直角顶点落在梯形的顶点C上，使三角板绕点C旋转．
（1）当三角板旋转到图1的位置时，猜想DE与BF的数量关系，并加以证明；
（2）在（1）问条件下，若BE：CE=1：2，∠BEC=135°，求sin∠BFE的值；
（3）当三角板的一边CF与梯形对角线AC重合时，作DH⊥PE于H，如图2，若OF=
时，求PE及DH的长．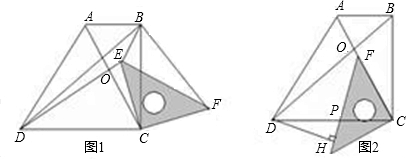
查看习题详情和答案>>
（1）当三角板旋转到图1的位置时，猜想DE与BF的数量关系，并加以证明；
（2）在（1）问条件下，若BE：CE=1：2，∠BEC=135°，求sin∠BFE的值；
（3）当三角板的一边CF与梯形对角线AC重合时，作DH⊥PE于H，如图2，若OF=
| ||
| 6 |
查看习题详情和答案>>
在梯形ABCD中，AB∥CD，∠BCD=90°，且AB=1，BC=2，tan∠ADC=2．对角线AC和BD相交于点O，等腰直角三角板的直角顶点落在梯形的顶点C上，使三角板绕点C旋转．
（1）如图1，当三角板旋转到点E落在BC边上时，线段DE与BF的位置关系是 ，数量关系是 ；
（2）继续旋转三角板，旋转角为α．请你在图2中画出图形，并判断（1）中结论还成立吗？如果成立请加以证明；如果不成立，请说明理由；
（3）如图3，当三角板的一边CF与梯形对角线AC重合时，EF与CD相交于点P，若OF=
，求PE的长．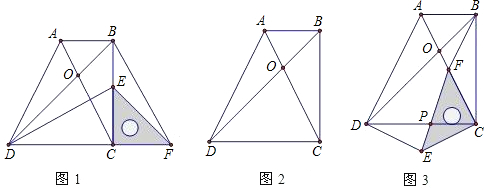
查看习题详情和答案>>
（1）如图1，当三角板旋转到点E落在BC边上时，线段DE与BF的位置关系是
（2）继续旋转三角板，旋转角为α．请你在图2中画出图形，并判断（1）中结论还成立吗？如果成立请加以证明；如果不成立，请说明理由；
（3）如图3，当三角板的一边CF与梯形对角线AC重合时，EF与CD相交于点P，若OF=
| ||
| 6 |
查看习题详情和答案>>
时，求PE及DH的长．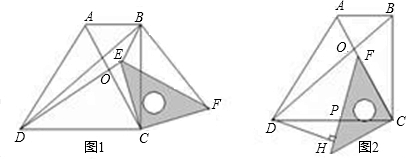
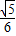时，求PE及DH的长．