摘要:小华是这样想的:因为CF和BE相交于点O.根据 .得∠COB=∠FOE.而0是CF的中点.那么CO=FO.又已知EO=BO.根据 .得△COB≌△FOE.所以BC=EF.∠BCO=∠F.又∠BCO=∠F.根据 .得AB∥DF.根据 .得∠ACE+∠DEC=180º.
网址:http://m.1010jiajiao.com/timu_id_736554[举报]
 28、如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.
28、如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.小华是这样想的:因为CF和BE相交于点O,
根据
对顶角相等
得出∠COB=∠EOF;而O是CF的中点,那么CO=FO,又已知EO=BO,
根据
两边对应相等且夹角相等的两三角形全等
得出△COB≌△FOE,根据
全等三角形对应边相等
得出BC=EF,根据
全等三角形对应角相等
得出∠BCO=∠F,既然∠BCO=∠F根据
内错角相等,两直线平行
、得出AB∥DF,既然AB∥DF,根据
两直线平行,同旁内角互补
.得出∠ACE和∠DEC互补.如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=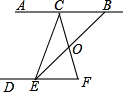 EF.以下是他的想法,请你填上根据.
EF.以下是他的想法,请你填上根据.
小华是这样想的:因为CF和BE相交于点O,
根据________,得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知EO=BO,
根据________,得出△COB≌△FOE,
根据________,得出BC=EF,
根据________,得出∠BCO=∠F,
既然∠BCO=∠F根据________,得出AB∥DF,
既然AB∥DF,根据________,得出∠ACE和∠DEC互补.
查看习题详情和答案>>
如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=

EF.以下是他的想法,请你填上根据.
小华是这样想的:因为CF和BE相交于点O,
根据______,得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知EO=BO,
根据______,得出△COB≌△FOE,
根据______,得出BC=EF,
根据______,得出∠BCO=∠F,
既然∠BCO=∠F根据______,得出AB∥DF,
既然AB∥DF,根据______,得出∠ACE和∠DEC互补.
查看习题详情和答案>>

EF.以下是他的想法,请你填上根据.
小华是这样想的:因为CF和BE相交于点O,
根据______,得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知EO=BO,
根据______,得出△COB≌△FOE,
根据______,得出BC=EF,
根据______,得出∠BCO=∠F,
既然∠BCO=∠F根据______,得出AB∥DF,
既然AB∥DF,根据______,得出∠ACE和∠DEC互补.
如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.
小华是这样想的:因为CF和BE相交于点O,
根据_________,得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知EO=BO,
根据_________________,得出△COB≌△FOE,
根据__________________,得出BC=EF,
根据___________________,得出∠BCO=∠F,
既然∠BCO=∠F根据_______________,得出AB∥DF,
既然AB∥DF,根据________________,得出∠ACE和∠DEC互补.
小华是这样想的:因为CF和BE相交于点O,
根据_________,得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知EO=BO,
根据_________________,得出△COB≌△FOE,
根据__________________,得出BC=EF,
根据___________________,得出∠BCO=∠F,
既然∠BCO=∠F根据_______________,得出AB∥DF,
既然AB∥DF,根据________________,得出∠ACE和∠DEC互补.
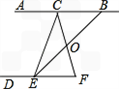
如图,直线AC∥DF,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结CF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF。
以下是他的想法,请你填上根据。小华是这样想的:
因为CF和BE相交于点O,
根据 得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知 EO=BO,
根据 得出△COB≌△FOE,
根据 得出BC=EF,
根据 得出∠BCO=∠F,
既然∠BCO=∠F,根据 出AB∥DF,
既然AB∥DF,根据 得出∠ACE和∠DEC互补.