摘要：按要求画图 请设计三种不同的方法.将如图所示直角三角形分割成四个小三角形.使得每个小三角形与原直角三角形都相似．(要求画出分割线段.标出能够说明分法的必要记号.不要求证明.不要求写画法).
网址：http://m.1010jiajiao.com/timu_id_736309[举报]
25、如图，一个圆形街心花园，有三个出口A、B、C，每两个出口之间有一条长60米的道路，组成正三角形ABC，在中心O处有一个亭子．为使亭子与原有的道路相通，需修三条小路OD、OE、OF，使另一出口D、E、F分别落在三角形的三边上，且这三条小道把三角形分成三个全等的多边形，以备种植不同的花草，
（1）请你按以上要求设计两种不同的方案．将你的设计方案分别画在图（a）、图（b）上，并附简单的说明；
（2）要使三条小道把三角形分成三个全等的等腰梯形，应怎样设计？把方案画在图（c）上，并简单说明画法（不需证明）；
（3）请你探究出一种一般方法，使得D不论在什么位置，都能准确找到另外两个出口E、F的位置，请写明这个画法．用图（d）表示出来．
（4）你在上图中探索出的一般方法是否适用于正方形？请结合图（e）予以说明；这种方法可以推广到正n边形吗？
查看习题详情和答案>>
（1）请你按以上要求设计两种不同的方案．将你的设计方案分别画在图（a）、图（b）上，并附简单的说明；
（2）要使三条小道把三角形分成三个全等的等腰梯形，应怎样设计？把方案画在图（c）上，并简单说明画法（不需证明）；
（3）请你探究出一种一般方法，使得D不论在什么位置，都能准确找到另外两个出口E、F的位置，请写明这个画法．用图（d）表示出来．
（4）你在上图中探索出的一般方法是否适用于正方形？请结合图（e）予以说明；这种方法可以推广到正n边形吗？
如图，一个圆形街心花园，有三个出口A、B、C，每两个出口之间有一条长60米的道路，组成正三角形ABC，在中心O处有一个亭子．为使亭子与原有的道路相通，需修三条小路OD、OE、OF，使另一出口D、E、F分别落在三角形的三边上，且这三条小道把三角形分成三个全等的多边形，以备种植不同的花草，
（1）请你按以上要求设计两种不同的方案．将你的设计方案分别画在图（a）、图（b）上，并附简单的说明；
（2）要使三条小道把三角形分成三个全等的等腰梯形，应怎样设计？把方案画在图（c）上，并简单说明画法（不需证明）；
（3）请你探究出一种一般方法，使得D不论在什么位置，都能准确找到另外两个出口E、F的位置，请写明这个画法．用图（d）表示出来．
（4）你在上图中探索出的一般方法是否适用于正方形？请结合图（e）予以说明；这种方法可以推广到正n边形吗？
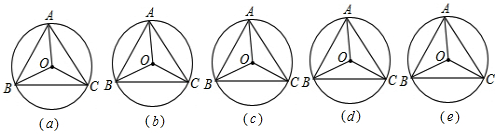
查看习题详情和答案>>
如图，一个圆形街心花园，有三个出口A、B、C，每两个出口之间有一条长60米的道路，组成正三角形ABC，在中心O处有一个亭子．为使亭子与原有的道路相通，需修三条小路OD、OE、OF，使另一出口D、E、F分别落在三角形的三边上，且这三条小道把三角形分成三个全等的多边形，以备种植不同的花草，
（1）请你按以上要求设计两种不同的方案．将你的设计方案分别画在图（a）、图（b）上，并附简单的说明；
（2）要使三条小道把三角形分成三个全等的等腰梯形，应怎样设计？把方案画在图（c）上，并简单说明画法（不需证明）；
（3）请你探究出一种一般方法，使得D不论在什么位置，都能准确找到另外两个出口E、F的位置，请写明这个画法．用图（d）表示出来．
（4）你在上图中探索出的一般方法是否适用于正方形？请结合图（e）予以说明；这种方法可以推广到正n边形吗？
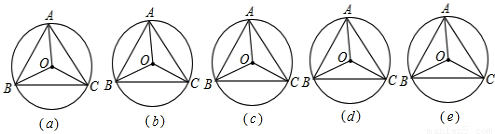
查看习题详情和答案>>
（1）请你按以上要求设计两种不同的方案．将你的设计方案分别画在图（a）、图（b）上，并附简单的说明；
（2）要使三条小道把三角形分成三个全等的等腰梯形，应怎样设计？把方案画在图（c）上，并简单说明画法（不需证明）；
（3）请你探究出一种一般方法，使得D不论在什么位置，都能准确找到另外两个出口E、F的位置，请写明这个画法．用图（d）表示出来．
（4）你在上图中探索出的一般方法是否适用于正方形？请结合图（e）予以说明；这种方法可以推广到正n边形吗？
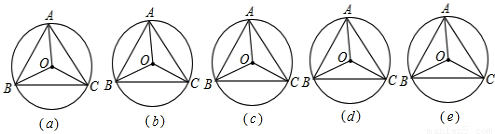
查看习题详情和答案>>
如图，正方形表示一张纸片，根据要求，需通过多次分割，将正方形纸片分割成若干个直角三角形，操作过程如下：第一次分割，将正方形纸片分成4个全等的直角三角形；第二次分割，将上次得到的直角三角形中的一个再分成4个全等直角三角形；以后按第二次分割的做法进行下去．
(1)请你设计出两种符合题意的分割方案图(要求在图1、图2中分别画出每种方案的第一次和第二次的分割线，只要有一条分割线段不同，就视为一种不同方案，图3供操作、实验用)．
(2)设正方形的边长为a，请你就其中一种方案通过操作和观察将第二、第三次分割后所得的最小直角三角形的面积S填入下表：
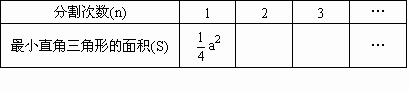
(3)在条件(2)下，请你猜想：分割所得的最小直角三角形的面积S与分割次数n有什么关系？用数学表达式表示出来．
查看习题详情和答案>>
【问题引入】
几个人拎着水桶在一个水龙头前面排队打水，水桶有大有小．他们该怎样排队才能使得总的排队时间最短？
假设只有两个人时，设大桶接满水需要T分钟，小桶接满水需要t分钟（显然T＞t），若拎着大桶者在拎着小桶者之前，则拎大桶者可直接接水，只需等候T分钟，拎小桶者一共等候了（T+t）分钟，两人一共等候了（2T+t）分钟；反之，若拎小桶者在拎大桶者前面，容易求出出两人接满水等候（T+2t）分钟．可见，要使总的排队时间最短，拎小桶者应排在拎大桶者前面．这样，我们可以猜测，几个人拎着水桶在一个水龙头前面排队打水，要使总的排队时间最短，需将他们按水桶从小到大排队．
规律总结：
事实上，只要不按从小到大的顺序排队，就至少有紧挨着的两个人拎着大桶者排在拎小桶者之前，仍设大桶接满水需要T分钟，小桶接满水需要t分钟，并设拎大桶者开始接水时已等候了m分钟，这样拎大桶者接满水一共等候了（m+T）分钟，拎小桶者一共等候了（m+T+t）分钟，两人一共等候了（2m+2T+t）分钟，在其他人位置不变的前提下，让这两个人交还位置，即局部调整这两个人的位置，同样介意计算两个人接满水共等候了______分钟，共节省了______分钟，而其他人等候的时间未变，这说明只要存在有紧挨着的两个人是拎大桶者在拎小桶者之前都可以这样调整，从而使得总等候时间减少．这样经过一系列调整后，整个队伍都是从小打到排列，就打到最优状态，总的排队时间就最短．
【方法探究】
一般的，对某些设计多个可变对象的数学问题，先对其少数对象进行调整，其他对象暂时保持不变，从而化难为易，取得问题的局部解决．经过若干次这种局部的调整，不断缩小范围，逐步逼近目标，最终使问题得到解决，这种数学思想就叫做局部调整法．
【实践应用1】
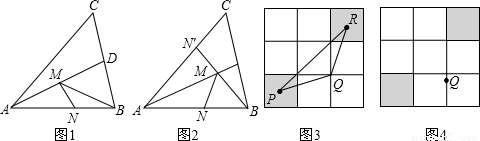
如图1在锐角△ABC中，AB=
，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是多少？
解析：
（1）先假定N为定点，调整M到合适的位置使BM+MN有最小值（相对的），容易想到，在AC上作AN′=AN（即作点N关于AD的对称点N'），连接BN′交AD于M，则M点是使BM+MN有相对最小值的点．（如图2，M点是确定方法找到的）
（2）在考虑点N的位置，使BM+MN最终达到最小值．可以理解，BM+MN=BM+MN′，所以要使BM+MN′有最小值，只需使______，此时BM+MN的最小值是______．
【实践应用2】
如图3，把边长是3的正方形等分成9个小正方形，在有阴影的小正方形内（包括边界）分别取点P、R，于已知格点Q（每个小正方形的顶点叫做格点）构成三角形，则△PQR的最大面积是______，请在图4中画出面积最大时的△PQR的图形．
查看习题详情和答案>>
几个人拎着水桶在一个水龙头前面排队打水，水桶有大有小．他们该怎样排队才能使得总的排队时间最短？
假设只有两个人时，设大桶接满水需要T分钟，小桶接满水需要t分钟（显然T＞t），若拎着大桶者在拎着小桶者之前，则拎大桶者可直接接水，只需等候T分钟，拎小桶者一共等候了（T+t）分钟，两人一共等候了（2T+t）分钟；反之，若拎小桶者在拎大桶者前面，容易求出出两人接满水等候（T+2t）分钟．可见，要使总的排队时间最短，拎小桶者应排在拎大桶者前面．这样，我们可以猜测，几个人拎着水桶在一个水龙头前面排队打水，要使总的排队时间最短，需将他们按水桶从小到大排队．
规律总结：
事实上，只要不按从小到大的顺序排队，就至少有紧挨着的两个人拎着大桶者排在拎小桶者之前，仍设大桶接满水需要T分钟，小桶接满水需要t分钟，并设拎大桶者开始接水时已等候了m分钟，这样拎大桶者接满水一共等候了（m+T）分钟，拎小桶者一共等候了（m+T+t）分钟，两人一共等候了（2m+2T+t）分钟，在其他人位置不变的前提下，让这两个人交还位置，即局部调整这两个人的位置，同样介意计算两个人接满水共等候了______分钟，共节省了______分钟，而其他人等候的时间未变，这说明只要存在有紧挨着的两个人是拎大桶者在拎小桶者之前都可以这样调整，从而使得总等候时间减少．这样经过一系列调整后，整个队伍都是从小打到排列，就打到最优状态，总的排队时间就最短．
【方法探究】
一般的，对某些设计多个可变对象的数学问题，先对其少数对象进行调整，其他对象暂时保持不变，从而化难为易，取得问题的局部解决．经过若干次这种局部的调整，不断缩小范围，逐步逼近目标，最终使问题得到解决，这种数学思想就叫做局部调整法．
【实践应用1】
如图1在锐角△ABC中，AB=
，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是多少？解析：
（1）先假定N为定点，调整M到合适的位置使BM+MN有最小值（相对的），容易想到，在AC上作AN′=AN（即作点N关于AD的对称点N'），连接BN′交AD于M，则M点是使BM+MN有相对最小值的点．（如图2，M点是确定方法找到的）
（2）在考虑点N的位置，使BM+MN最终达到最小值．可以理解，BM+MN=BM+MN′，所以要使BM+MN′有最小值，只需使______，此时BM+MN的最小值是______．
【实践应用2】
如图3，把边长是3的正方形等分成9个小正方形，在有阴影的小正方形内（包括边界）分别取点P、R，于已知格点Q（每个小正方形的顶点叫做格点）构成三角形，则△PQR的最大面积是______，请在图4中画出面积最大时的△PQR的图形．
查看习题详情和答案>>