网址:http://m.1010jiajiao.com/timu_id_73607[举报]
一、选择题
DCADC ACBDB AC
二、填空题:
13. 3
14. -10 15. -1 16..files/image177.gif)
三、解答题:
17.解; (I)
.files/image179.gif)
它的最小正周期.files/image181.gif)
(II)由(I)及.files/image130.gif) 得,
得,
.files/image184.gif)
.files/image186.gif)
由正弦定理,得.files/image188.gif)
18.解法一
(I)由已知。BC//AE,则AE与SB所成的角等于BC与SB所成的角。
连结SC. 由题设,.files/image190.gif) 为直二面角S-AE-C的平面角,于是EA、EC、ES两两互相垂直。
为直二面角S-AE-C的平面角,于是EA、EC、ES两两互相垂直。
在.files/image192.gif) 中,
中,.files/image194.gif) 则
则.files/image196.gif)
在.files/image198.gif) 中,
中, .files/image200.gif) 则
则.files/image202.gif)
易见,.files/image204.gif) 平面
平面.files/image206.gif) , 则
, 则.files/image208.gif) 平面
平面.files/image206.gif) ,从而
,从而.files/image211.gif)
在.files/image213.gif) 中,
中,.files/image215.gif)
所以AE与SB所成角的大小为.files/image217.gif)
(II).files/image219.gif) 平面
平面.files/image221.gif) ,
,.files/image223.gif) 平面
平面.files/image225.gif) 平面
平面.files/image221.gif)
作.files/image227.gif) 于O,则
于O,则.files/image229.gif) 平面
平面.files/image231.gif) ,作
,作.files/image233.gif) 于F,连结AF, 则
于F,连结AF, 则.files/image235.gif)
.files/image237.gif) 为二面角A-SB-E的平面角
为二面角A-SB-E的平面角
在.files/image239.gif) 中,
中,.files/image241.gif)
因为.files/image243.gif) ,所以
,所以.files/image245.gif) ,则
,则.files/image247.gif)
.files/image249.gif)
故二面角A-SB-E的大小为.files/image251.gif)
.files/image253.jpg)
解法二:
(I)有题设,为直二面角S-AE-C的平面角,于是EA、EC、ES两两互相垂直,
建立如图所示的空间直角坐标系.files/image255.gif) ,其中,
,其中,
.files/image257.gif)
.files/image259.gif)
.files/image261.gif)
所以,AE与SB所成角的大小为.files/image263.gif)
(II)设.files/image265.gif) 为,面SBE的法向量,则
为,面SBE的法向量,则.files/image267.gif) ,且
,且.files/image269.gif)
.files/image271.gif)
设.files/image273.gif) 为面SAB的法向量,则
为面SAB的法向量,则.files/image275.gif) ,且
,且.files/image277.gif)
.files/image279.gif)
以内二面角A-SB-E为锐角,所以其大小为.files/image281.gif)
19.解:
(I)5位旅客在A、B、C三个景点的下车的方法种数为.files/image283.gif) ,其中在A景点不停车即知在B、C景点停车的为方程种数为
,其中在A景点不停车即知在B、C景点停车的为方程种数为.files/image283.gif) 。
。
所以游车在A景点不停的概率
.files/image285.gif)
(II)记事件“游车在三个景点停一次车”为E,则
.files/image287.gif)
所以游车至少停两次的概率为
.files/image289.gif)
20.解:
(I).files/image291.gif)
由已知,得.files/image293.gif) ,
,
在由切点为.files/image295.gif) ,
,
.files/image297.gif)
(II).files/image299.gif)
.files/image301.gif) 方程有两个不相等的实根
方程有两个不相等的实根.files/image303.gif)
而.files/image305.gif) ,则方程的负根
,则方程的负根.files/image307.gif)
依题意,.files/image309.gif) 即只需
即只需.files/image311.gif) ,解得
,解得.files/image313.gif)
当.files/image315.gif) 时,
时,.files/image124.gif) 单调递增,当
单调递增,当.files/image318.gif) 时,
时,.files/image124.gif) 单调递减,所以
单调递减,所以.files/image124.gif) 在
在.files/image320.gif) 处取得极大值。
处取得极大值。
因此.files/image016.gif) 的取值范围是
的取值范围是.files/image323.gif)
21.解:
(I).files/image325.gif)
当.files/image327.gif) 时,
时,.files/image329.gif) 且对于
且对于.files/image331.gif) 也成立
也成立
所以.files/image333.gif)
.files/image335.gif)
由.files/image337.gif)
.files/image339.gif)
(II)
.files/image341.gif)
.files/image343.gif) ①
①
.files/image345.gif) ②
②
① -②,得
.files/image347.gif)
22..解:
由.files/image169.gif) ,得
,得.files/image350.gif) ,代入
,代入.files/image352.gif) ,得
,得.files/image354.gif)
设.files/image356.gif) ,则
,则.files/image358.gif) 是这个一元二次方程的两个根,
是这个一元二次方程的两个根,
.files/image360.gif) ①
①
由.files/image362.gif) ,及
,及.files/image364.gif) ,得
,得.files/image366.gif)
由根与系数的关系,得
.files/image368.gif) ②
②
.files/image370.gif) ③
③
由②式得.files/image372.gif) ,代入③式,得
,代入③式,得.files/image374.gif)
.files/image376.gif) ④
④
由.files/image378.gif) ,及①、④,得
,及①、④,得.files/image380.gif)
解不等式组,得.files/image382.gif)
所以.files/image016.gif) 的取值范围是
的取值范围是.files/image385.gif)
已知函数f(x)=asinx-x+b(a>0,b>0).
(1)求证:函数f(x)在区间[0,a+b]内至少有一个零点;
(2)若函数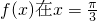 处取得极值.
处取得极值.
(i)不等式f(x)>sinx+cosx对任意 恒成立,求b的取值范围;
恒成立,求b的取值范围;
(ii)设△ABC的三个顶点A(x1,y1),B(x2,y2),C(x3,y3)在函数f(x)的图象上,且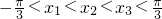 ,求证:f(sin2A+sin2C)<f(sin2B).
,求证:f(sin2A+sin2C)<f(sin2B).
查看习题详情和答案>>
(1)求证:函数f(x)在区间[0,a+b]内至少有一个零点;
(2)若函数
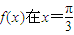 处取得极值.
处取得极值.(i)不等式f(x)>sinx+cosx对任意
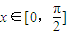 恒成立,求b的取值范围;
恒成立,求b的取值范围;(ii)设△ABC的三个顶点A(x1,y1),B(x2,y2),C(x3,y3)在函数f(x)的图象上,且
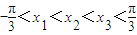 ,求证:f(sin2A+sin2C)<f(sin2B).
,求证:f(sin2A+sin2C)<f(sin2B).查看习题详情和答案>>
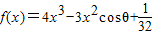 ,其中x∈R,θ为参数,且0≤θ≤
,其中x∈R,θ为参数,且0≤θ≤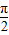 .
.(Ⅰ)当cosθ=0时,判断函数f(x)是否有极值;
(Ⅱ)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(Ⅲ)若对(II)中所求的取值范围内的任意参数θ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
查看习题详情和答案>>
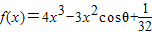 ,其中x∈R,θ为参数,且0≤θ≤
,其中x∈R,θ为参数,且0≤θ≤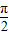 .
.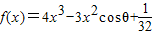 ,其中x∈R,θ为参数,且0≤θ≤
,其中x∈R,θ为参数,且0≤θ≤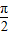 .
.