题目内容
已知函数 ,其中x∈R,θ为参数,且0≤θ≤
,其中x∈R,θ为参数,且0≤θ≤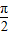 .
.(Ⅰ)当cosθ=0时,判断函数f(x)是否有极值;
(Ⅱ)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(Ⅲ)若对(II)中所求的取值范围内的任意参数θ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
【答案】分析:(1)先求函数的导数,f′(x)>0在(-∞,+∞)上恒成立,得到函数的单调性,从而可判定是否有极值.
(2)先求出极值点,f′(x)=0的点附近的导数的符号的变化情况,来确定极值,求出极小值,使函数f(x)的极小值大于零建立不等关系,求出参数θ的取值范围即可.
(3)由(II)知,函数f(x)在区间(-∞,0)与 内都是增函数,只需(2a-1,a)是区间(-∞,0)与
内都是增函数,只需(2a-1,a)是区间(-∞,0)与 的子集即可.
的子集即可.
解答:解:(I)解:当cosθ=0时 ,则f(x)在(-∞,+∞)内是增函数,
,则f(x)在(-∞,+∞)内是增函数,
故无极值.
(II)解:f'(x)=12x2-6xcosθ,令f'(x)=0,
得 .
.
由 及(I),只需考虑cosθ>0的情况.
及(I),只需考虑cosθ>0的情况.
当x变化时,f'(x)的符号及f(x)的变化情况如下表:
因此,函数f(x)在 处取得极小值
处取得极小值 ,且
,且 .
.
要使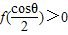 ,必有
,必有 ,
,
可得 ,所以
,所以
(III)解:由(II)知,函数f(x)在区间(-∞,0)与 内都是增函数.
内都是增函数.
由题设,函数f(x)在(2a-1,a)内是增函数,
则a须满足不等式组 或
或
由(II),参数 时,
时, .要使不等式
.要使不等式 关于参数θ恒成立,必有
关于参数θ恒成立,必有 .
.
综上,解得a≤0或 .
.
所以a的取值范围是 .
.
点评:本小题主要考查运用导数研究函数的单调性及极值、解不等式等基础知识,考查综合分析和解决问题的能力.
(2)先求出极值点,f′(x)=0的点附近的导数的符号的变化情况,来确定极值,求出极小值,使函数f(x)的极小值大于零建立不等关系,求出参数θ的取值范围即可.
(3)由(II)知,函数f(x)在区间(-∞,0)与
 内都是增函数,只需(2a-1,a)是区间(-∞,0)与
内都是增函数,只需(2a-1,a)是区间(-∞,0)与 的子集即可.
的子集即可.解答:解:(I)解:当cosθ=0时
 ,则f(x)在(-∞,+∞)内是增函数,
,则f(x)在(-∞,+∞)内是增函数,故无极值.
(II)解:f'(x)=12x2-6xcosθ,令f'(x)=0,
得
 .
.由
 及(I),只需考虑cosθ>0的情况.
及(I),只需考虑cosθ>0的情况.当x变化时,f'(x)的符号及f(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0, ) ) |  | ( ) ) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
 处取得极小值
处取得极小值 ,且
,且 .
.要使
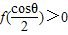 ,必有
,必有 ,
,可得
 ,所以
,所以
(III)解:由(II)知,函数f(x)在区间(-∞,0)与
 内都是增函数.
内都是增函数.由题设,函数f(x)在(2a-1,a)内是增函数,
则a须满足不等式组
 或
或
由(II),参数
 时,
时, .要使不等式
.要使不等式 关于参数θ恒成立,必有
关于参数θ恒成立,必有 .
.综上,解得a≤0或
 .
.所以a的取值范围是
 .
.点评:本小题主要考查运用导数研究函数的单调性及极值、解不等式等基础知识,考查综合分析和解决问题的能力.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为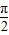 ,且图象上一个点为
,且图象上一个点为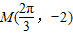 .
.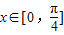 恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围. (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为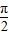 ,且图象上一个点为
,且图象上一个点为 .
. 求函数f(x)的值域;
求函数f(x)的值域;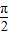 个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.
个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.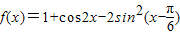 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )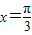
 的图象左移
的图象左移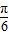 得到函数f(x)的图象
得到函数f(x)的图象 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移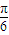 得到函数f(x)的图象
得到函数f(x)的图象 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象