摘要:5组中值(分)
网址:http://m.1010jiajiao.com/timu_id_733410[举报]
(1)计算:2-1+20070+
+tan45°;
(2)化简求值:(1+
)•(x2-1),其中x=
.
(3)在数学上,对于两个数p和q有三种平均数,即算术平均数A、几何平均数G、调和平均数H,其中A=
,G=
.而调和平均数中的“调和”二字来自于音乐,毕达哥拉斯学派通过研究发现,如果三根琴弦的长度p=10,H=12,q=15满足
-
=
-
,再把它们绷得一样紧,并用同样的力弹拨,它们将会分别发出很调和的乐声.我们称p、H、q为一组调和数,而把H称为p和q的调和平均数.
①若p=2,q=6,则A= ,G= .
②根据上述关系,用p、q的代数式表示出它们的调和平均数H;并根据你所得到的结论,再写出一组调和数. 查看习题详情和答案>>
| 1 | ||
|
(2)化简求值:(1+
| 1 |
| x-1 |
| 1 |
| 3 |
(3)在数学上,对于两个数p和q有三种平均数,即算术平均数A、几何平均数G、调和平均数H,其中A=
| p+q |
| 2 |
| pq |
| 1 |
| 10 |
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 15 |
①若p=2,q=6,则A=
②根据上述关系,用p、q的代数式表示出它们的调和平均数H;并根据你所得到的结论,再写出一组调和数. 查看习题详情和答案>>
(1)先化简,再求值:
×
,其中x=2;
(2)某学习小组共8人,在一次数学测验中,成绩(单位:分)分别为:100、74、90、74、74、90、74、64,试求这个小组的平均成绩. 查看习题详情和答案>>
| x |
| x2-1 |
| x2+x |
| x2 |
(2)某学习小组共8人,在一次数学测验中,成绩(单位:分)分别为:100、74、90、74、74、90、74、64,试求这个小组的平均成绩. 查看习题详情和答案>>
(1)如果△ABC的面积是S,E是BC的中点,连接AE(图1),则△AEC的面积是 ;
(2)在△ABC的外部作△ACD,F是AD的中点,连接CF(图2),若四边形ABCD的面积是S,则四边形AECF的面积是 ;
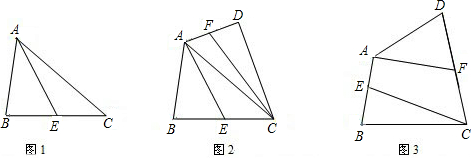
(3)若任意四边形ABCD的面积是S,E、F分别是一组对边AB,CD的中点,连接AF,CE(图3),则四边形AECF的面积是 .
拓展与应用
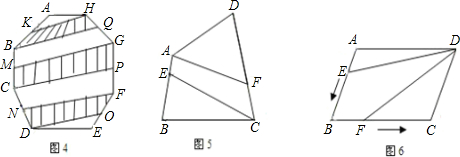
(1)若八边形ABCDEFGH的面积是100,K,M,N,O,P,Q分别是AB,BC,CD,EF,FG,GH的中点,连接KH,MG,NF,OD,PC,QB(图4),则图中阴影部分的面积是 ;
(2)四边形ABCD的面积是100,E,F分别是一组对边AB,CD上的点,且AE=
AB,CF=
CD,连接AF,CE(图5),则四边形AECF的面积是 .
(3)?ABCD的面积为2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动.点F从点B出发沿BC以每秒
个单位的速度向点C运动.E、F分别从点A,B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
查看习题详情和答案>>
(2)在△ABC的外部作△ACD,F是AD的中点,连接CF(图2),若四边形ABCD的面积是S,则四边形AECF的面积是

(3)若任意四边形ABCD的面积是S,E、F分别是一组对边AB,CD的中点,连接AF,CE(图3),则四边形AECF的面积是
拓展与应用
(1)若八边形ABCDEFGH的面积是100,K,M,N,O,P,Q分别是AB,BC,CD,EF,FG,GH的中点,连接KH,MG,NF,OD,PC,QB(图4),则图中阴影部分的面积是
(2)四边形ABCD的面积是100,E,F分别是一组对边AB,CD上的点,且AE=
| 1 |
| 3 |
| 1 |
| 3 |

(3)?ABCD的面积为2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动.点F从点B出发沿BC以每秒
| bv |
| a |