摘要：25．如图:已知:∠BAG与∠AGD互补.∠l=∠2 试问:∠E与∠F相等吗?为什么?
网址：http://m.1010jiajiao.com/timu_id_731032[举报]
如图，已知六边形ABCDEF与六边形GHIJKL相似，点A、B、C、D、E和F的对应点分别是点G、H、I、J、K和L．若它们的相似比为2：1，则下列结论中，正确的是（ ）
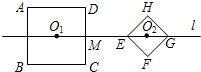如图，已知正方形ABCD与正方形EFGH的边长分别是4| 2 |
| 2 |
| 2 |
（1）在开始运动前，O1O2=
（2）当两个正方形按照各自的运动方式同时运动3秒时，正方形ABCD停止旋转，这时AE=
（3）当正方形ABCD停止旋转后，正方形EFGH继续向左平移的时间为x秒，两正方形重叠部分的面积为y，求y与x之间的函数表达式． 查看习题详情和答案>>
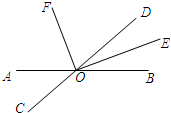如图，已知直线AB与CD相交于点O，OE、OF分别是∠BOD、∠AOD的平分线．（1）∠DOE的补角是
∠AOE或∠COE
∠AOE或∠COE
；（2）若∠BOD=62°，求∠AOE和∠DOF的度数；
（3）判断射线OE与OF之间有怎样的位置关系？并说明理由．
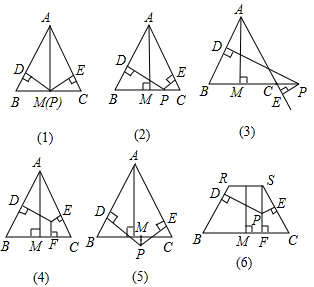
（2007•临夏州）[（1）-（3），10分]如图，已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为h1、h2、h3，△ABC的高为h．
在图（1）中，点P是边BC的中点，此时h3=0，可得结论：h1+h2+h3=h．
在图（2）--（5）中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图（2）--（5）中，h1、h2、h3、h之间的关系；（直接写出结论）
（2）证明图（2）所得结论；
（3）证明图（4）所得结论．
（4）在图（6）中，若四边形RBCS是等腰梯形，∠B=∠C=60°，RS=n，BC=m，点P在梯形内，且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4，桥形的高为h，则h1、h2、h3、h4、h之间的关系为：
查看习题详情和答案>>
在图（1）中，点P是边BC的中点，此时h3=0，可得结论：h1+h2+h3=h．
在图（2）--（5）中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图（2）--（5）中，h1、h2、h3、h之间的关系；（直接写出结论）
（2）证明图（2）所得结论；
（3）证明图（4）所得结论．
（4）在图（6）中，若四边形RBCS是等腰梯形，∠B=∠C=60°，RS=n，BC=m，点P在梯形内，且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4，桥形的高为h，则h1、h2、h3、h4、h之间的关系为：
m（h1+h2+h3）-n（h1+h3-h4）=（m+n）h
m（h1+h2+h3）-n（h1+h3-h4）=（m+n）h
；图（4）与图（6）中的等式有何关系？
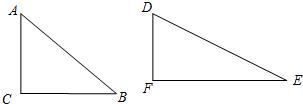27、如图，已知RT△ABC与RT△DEF不相似，其中∠C、∠F为直角，能否分别将这两个三角形各分割成两个三角形，使△ABC所分的每个三角形与△DEF所分成的每个三角形分别对应相似？若能，请设计出一种分割方案．