题目内容
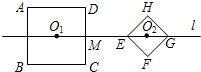 如图,已知正方形ABCD与正方形EFGH的边长分别是4
如图,已知正方形ABCD与正方形EFGH的边长分别是4| 2 |
| 2 |
| 2 |
(1)在开始运动前,O1O2=
(2)当两个正方形按照各自的运动方式同时运动3秒时,正方形ABCD停止旋转,这时AE=
(3)当正方形ABCD停止旋转后,正方形EFGH继续向左平移的时间为x秒,两正方形重叠部分的面积为y,求y与x之间的函数表达式.
分析:(1)开始运动前O1O2=O1M+ME+O2E,O1M=
AD=2
,O2E=
EH=2,因此O1O2=9.
(2)当运动3秒后,A在直线l上,O1A=
AD=4,O1E=7-3=4,因此O1E=O1A,A、E重合,即AE=0.
O1O2=O1A+O2E=4+2=6.
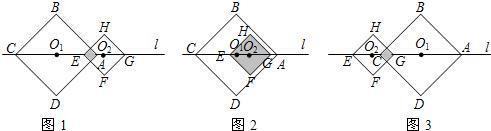
(3)本题要分四种情况:
①当0≤x<4时,图1,重合的小正方形对角线AE=x,因此y=
x2.
②当4≤x<8时,图2,正方形EFGH在正方形ABCD内部,重合部分的面积就是正方形EFGH的面积.
③当8≤x<12时,图3,参照①的解法.
④当x≥12时,此时两正方形不重合,因此y=0.
| 1 |
| 2 |
| 2 |
| ||
| 2 |
(2)当运动3秒后,A在直线l上,O1A=
| ||
| 2 |
O1O2=O1A+O2E=4+2=6.
(3)本题要分四种情况:
①当0≤x<4时,图1,重合的小正方形对角线AE=x,因此y=
| 1 |
| 2 |
②当4≤x<8时,图2,正方形EFGH在正方形ABCD内部,重合部分的面积就是正方形EFGH的面积.
③当8≤x<12时,图3,参照①的解法.
④当x≥12时,此时两正方形不重合,因此y=0.
解答:解:(1)9.
(2)0,6
(3)当正方形ABCD停止运动后,正方形EFGH继续向左平移时,与正方形ABCD重叠部分的形状也是正方形.
重叠部分的面积y与x之间的函数关系应分四种情况:
①如图1,当0≤x<4时,
∵EA=x,
∴y与x之间的函数关系式为y=
.
②如图2,当4≤x<8时,y与x之间的函数关系式为y=(2
)2=8.
③如图3,当8≤x<12时,
∵CG=12-x,
∴y与x之间的函数关系式为y=
=
x2-12x+72.
④当x≥12时,y与x之间的函数关系式为y=0.
(2)0,6

(3)当正方形ABCD停止运动后,正方形EFGH继续向左平移时,与正方形ABCD重叠部分的形状也是正方形.
重叠部分的面积y与x之间的函数关系应分四种情况:
①如图1,当0≤x<4时,
∵EA=x,
∴y与x之间的函数关系式为y=
| x2 |
| 2 |
②如图2,当4≤x<8时,y与x之间的函数关系式为y=(2
| 2 |
③如图3,当8≤x<12时,
∵CG=12-x,
∴y与x之间的函数关系式为y=
| (12-x)2 |
| 2 |
| 1 |
| 2 |
④当x≥12时,y与x之间的函数关系式为y=0.
点评:本题为运动性问题,考查了正方形的性质、图形的旋转、二次函数的应用等知识.综合性强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
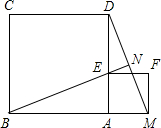 如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上,直线BE与DM交于点N.求证:BN⊥DM.
如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上,直线BE与DM交于点N.求证:BN⊥DM. (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( )
如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( ) 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.