摘要:17.已知点P(a.b)是平面直角坐标系中第二象限的点.则化简| a―b |+| b―a |的结果是 .
网址:http://m.1010jiajiao.com/timu_id_731022[举报]
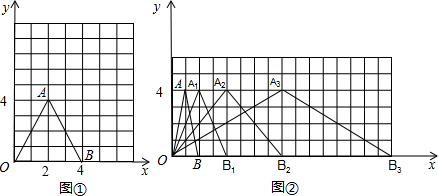
在平面直角坐标系中,图①和图②中的各三角形顶点均在网格图的格点上,根据所给信息解答下列问题:
(1)动手操作,探究结论:在图①中,△ABO的三个顶点的坐标分别是A(2,4)、B(4,0)、O(0,0),将△ABO的三个顶点的横坐标都加上2,纵坐标不变,分别得到点A’、B’、O’,依次连接A’、B’、O’各点,画出△A’B’O’,并说明△A’B’O’与△ABO在大小、形状、位置上有什么关系?
(2)仔细观察,探究规律:在图②中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0)B2(8,0),B3(16,0)…
①按此图形变化规律,写出△OA4B4的顶点坐标A4 ,B4 ;
②通过计算得出△OA4B4的面积是△OAB面积的 倍;
③通过上述变化规律,请你猜想出△OAnBn的面积是△OAB面积的多少倍?
 查看习题详情和答案>>
查看习题详情和答案>>
(1)动手操作,探究结论:在图①中,△ABO的三个顶点的坐标分别是A(2,4)、B(4,0)、O(0,0),将△ABO的三个顶点的横坐标都加上2,纵坐标不变,分别得到点A’、B’、O’,依次连接A’、B’、O’各点,画出△A’B’O’,并说明△A’B’O’与△ABO在大小、形状、位置上有什么关系?
(2)仔细观察,探究规律:在图②中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0)B2(8,0),B3(16,0)…
①按此图形变化规律,写出△OA4B4的顶点坐标A4
②通过计算得出△OA4B4的面积是△OAB面积的
③通过上述变化规律,请你猜想出△OAnBn的面积是△OAB面积的多少倍?
 查看习题详情和答案>>
查看习题详情和答案>>
在平面直角坐标系中,已知三点A(0,a),B(b,0),C(b,c),其中a,b,c满足关系式|a-2|+(b-3)2=0,c=2b-a;
(1)求a,b,c的值.
(2)如果在第二象限内有一点P(m,1),请用含m的式子表示四边形ABOP的面积;若四边形ABOP的面积与△ABC的面积相等,请求出点P的坐标;
附加题:
(3)若B,A两点分别在x轴,y轴的正半轴上运动,设∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q,那么,点A,B在运动的过程中,∠AQB的大小是否会发生变化?若不发生变化,请求出其值,若发生变化,请说明理由.
(4)是否存在一点N(n,-1),使AN+NC距离最短?如果有,请求出该点坐标,如果没有,请说明理由.
查看习题详情和答案>>
(1)求a,b,c的值.
(2)如果在第二象限内有一点P(m,1),请用含m的式子表示四边形ABOP的面积;若四边形ABOP的面积与△ABC的面积相等,请求出点P的坐标;
附加题:
(3)若B,A两点分别在x轴,y轴的正半轴上运动,设∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q,那么,点A,B在运动的过程中,∠AQB的大小是否会发生变化?若不发生变化,请求出其值,若发生变化,请说明理由.
(4)是否存在一点N(n,-1),使AN+NC距离最短?如果有,请求出该点坐标,如果没有,请说明理由.